目次へ

>> 序，１，２，３，４，５，６，７，８，９，10，11

ポートフォリオの期待リターン２　「証券がｎ個の場合」


前回までは２つの株式のポートフォリオを考えましたが、今回からは銘柄がもっと多い場合に話を拡張します。第１回で「個別株の情報がどう与えられるか」を、５種類の株式があるという設定で勉強しましたので、今日はその設定を用いて、５種類の株式に投資することを考えましょう。


それぞれの株のリターンを R_1，\cdots，R_5 とおきます。これらは確率変数です。


確率変数は値がいくつと出るか不確実ですが、期待値は推定できます。今、月次の期待リターンが以下の表のように分かっているとしましょう。（期待値はふつう E[\hspace{2mm}] または \mu を使って表すので、両方を記しておきます。）


これら５つの株式でポートフォリオを作った場合、その期待リターンはいくつになるか、というのが今回考えたい問いです。以下の表のようなウェイトのポートフォリオを考えましょう（ウェイトは w で表します）。投資資金のうち、たとえばA社に40%，E社には5%を投資するということです。


ウェイトは確率変数ではなく、投資家が自ら決める値であることに注意してください。各銘柄の期待リターン（緑の数字）が分かっており、かつ投資家が各銘柄へのウェイト（赤い数字）を決めたら、そのポートフォリオの期待リターンが決まります。それは「線型結合の期待値」の公式で求まります。


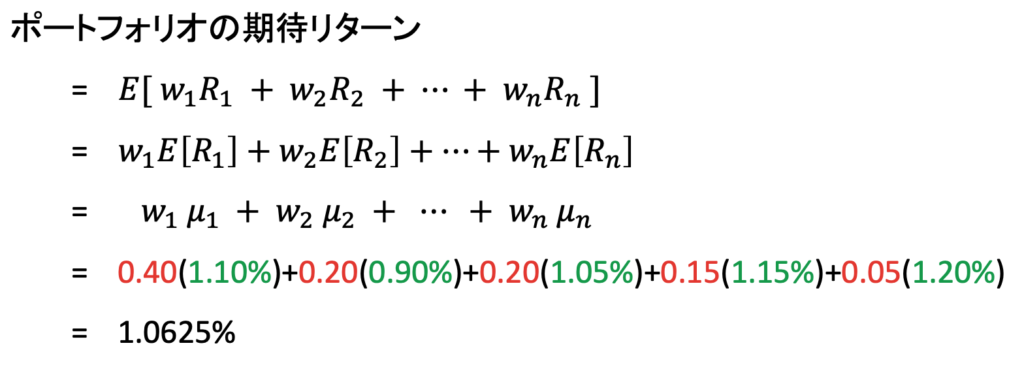
ポートフォリオのリターンは w_1R_1 + w_2R_2 + \cdots + w_5R_5 ですから、それに E[\; ] を付けたものがポートフォリオの期待リターンです（１つめのイコール）。
２つめのイコールは、「線型結合の期待値」の公式です。
３つめのイコールは、期待値を \mu で表した場合です。
４つめのイコールは、与えられた数値を代入しています。（ウェイトは、パーセントから小数に直してあります。）
最後のイコールのあとが答えです。このポートフォリオの期待リターンはおよそ1.06%となります。


株式が何種類あろうと、ポートフォリオの期待リターンは、各株の期待リターンの「加重平均」なのです。濃度の異なる食塩水を混ぜたとき、出来上がった食塩水の濃度はいくらかという話と同じです。でも、この「食塩水の法則」は、リスクに関しては当てはまらないということでした。次回は、ポートフォリオのリスクについて、ｎ種類の株式がある設定で解説したいと思います。

>> 平均分散分析（７）ポートフォリオのリターンの標準偏差２　「証券がｎ個の場合」