個別株の情報（リスク）
前回に引き続き、A，B，C，D，Eという５種類の株式があるとします。投資マネージャーに電話したあなたが、期待リターンの次に聞くべき情報は「リスク」です。でもリスクとは何でしょう。
「期待リターン1％」と言ったときの1％は、あくまで平均的なことが起こった場合の数字です。実際には株価は3％上がるかもしれないし、5％下がるかもしれない。毎月20％上がったり下がったりする、価格変動の激しい銘柄もあります。そのような状況では、期待値からの標準的なズレを表す「標準偏差」がリスクの情報として有用です。確率変数が5個あるので、標準偏差も5個あります。それらを並べた物が「標準偏差ベクトル」です。
上の例では、A社株のリターンの標準偏差は17％，B社株の方は11.4％と推定されています。日々データの収集と分析にあけくれる投資マネージャーにとって、リターンの標準偏差をあなたに教えることは容易いことです。しかしながら、実は５つの標準偏差だけではリスクの情報としては不十分なのです。その理由を説明しましょう。
５つの株にそれぞれどれだけ投資するか決めるに際して、A社株のリターンやB社株のリターンが単体としてどれくらい不確実なのか、それだけを知っても十分ではありません。A社株とB社株の連動性も知る必要があります。A社が不調のとき、B社もまた不調になる可能性が高いのでしょうか。それとも、A社が不調のときは、B社は好調である可能性が高いのでしょうか。「たくさんの卵を１つのカゴに入れて運ぶな」と言いますが、５つの株が、実際にはどれくらい離れた「カゴ」なのかが分からないと、効果的な分散投資はできません。そういうわけで、５つの株のリターン相互の、「相関係数」も重要な情報なのです。あなたは投資マネージャーに、５つの株の互いの相関も聞くべきです。
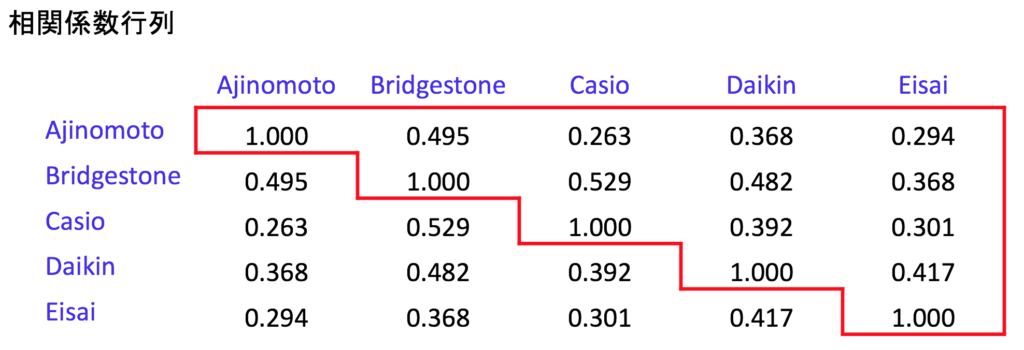
上の例では、投資マネージャーは、「A社とC社のリターンの相関係数は 0.263，B社とC社の場合は 0.529」と推定しています。相関係数を表の形に並べた行列を「相関行列 (correlation matrix)」と言います。このように、リスクの情報は「標準偏差ベクトル」と「相関行列」によって与えられるのです。
数字として直観的なのは「標準偏差と相関係数」なのですが、情報量としては「分散と共分散」でも一緒です。そして、このあとの計算にすぐ使えるのも、分散と共分散の方です。分散と共分散を規則正しく並べた行列を「分散共分散行列」といいます。
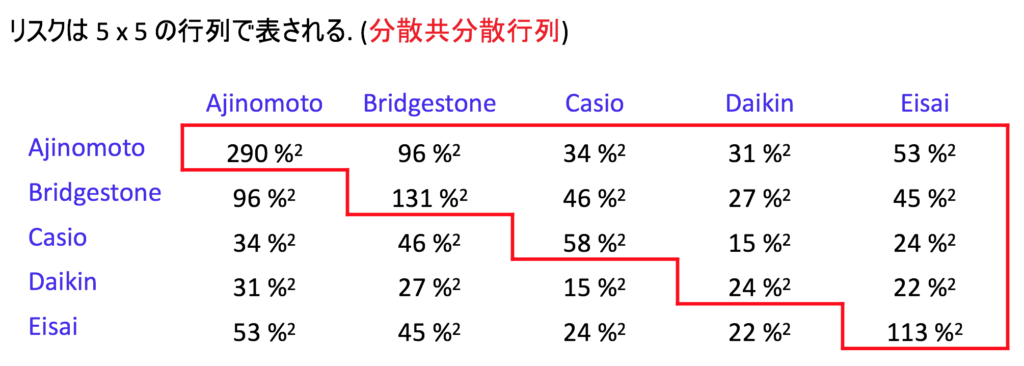
左上から右下にかけての対角線上には分散が並び、対角線から外れたところに共分散が並びます。例えば上から２行目、左から３列目の46
は、B社株のリターンとC社株のリターンの間の共分散を表しています。
まとめると、「５種類の株式があったら、期待値は5個数字が並んだ期待値ベクトル、リスクは 
の分散共分散行列」です。次回から、これら複数の株式を組み合わせてポートフォリオを作成します。
> マーコウィッツの平均分散分析（３）ポートフォリオの期待リターン１ 「証券が２つの場合」