リスク・リターン・フロンティア1 「証券が2個の場合」
今日のテーマは、ポートフォリオ・ウェイトを変えたとき、ポートフォリオのリスクとリターンがどのように変化するか、という問いです。
前回に引き続き、株式の銘柄が2つしかない状況を考えてください。トヨタの株が証券1、マクドナルドの株が証券2です。それぞれの期待リターンは ![]() ,
,![]() で,標準偏差は
で,標準偏差は ![]() ,
,![]() で表します。最後に、2つのリターンの相関係数は
で表します。最後に、2つのリターンの相関係数は ![]() で表します。これらの情報は全て与えられていると仮定します。
で表します。これらの情報は全て与えられていると仮定します。
2つの株のポートフォリオを考えます。ウェイトの和は1なので、トヨタのウェイトを ![]() とおいて、マクドナルドの方は
とおいて、マクドナルドの方は ![]() とおきます。そうすると、第3回の議論から、ポートフォリオのリターンの期待値は
とおきます。そうすると、第3回の議論から、ポートフォリオのリターンの期待値は
![]()
分散は、前回の議論より
![]()
となります。
たくさん文字が出てきますが、投資家が決められるのは
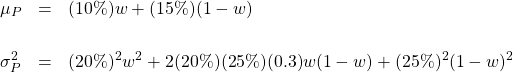
となり、
そこで、縦軸にポートフォリオのリターンの期待値、横軸に標準偏差(分散のルートを取ったもの)を取り、
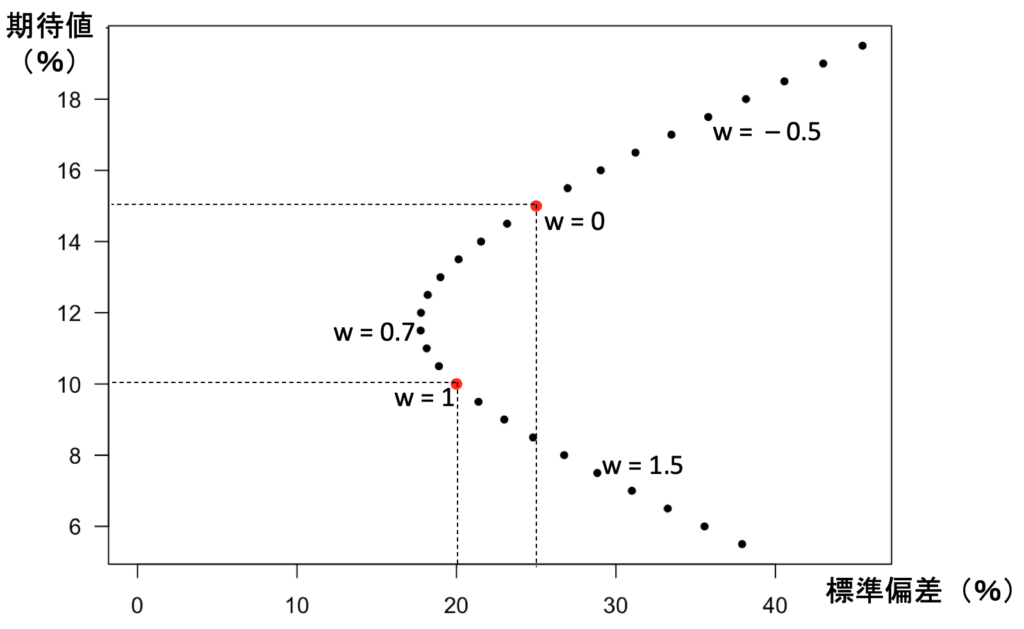
証券1(トヨタ)は ![]() ,証券2(マクドナルド)は
,証券2(マクドナルド)は ![]() でした。この2つの点は、図の中では赤い点で表されており、それぞれ
でした。この2つの点は、図の中では赤い点で表されており、それぞれ ![]() と
と ![]() に対応します。
に対応します。![]() は証券1のウェイトなので、これがマイナスの場合は、証券1を空売りして得た現金でさらに証券2を買い足していることを意味します。
は証券1のウェイトなので、これがマイナスの場合は、証券1を空売りして得た現金でさらに証券2を買い足していることを意味します。
注意して欲しいのは標準偏差の方です。証券1は20%、証券2は25%ですが、それならば証券1に全額投資したときが標準偏差が最小になるかというと、そうではありません。このグラフの中には、「相関が0.3」という情報が現れていないので忘れがちですが、前回の内容を思い出してください。2つの証券のリターンが完全相関していない場合なので、両方に分けて投資することで、「分散投資効果」が働くのです。
この例では ![]() の点でリターンの標準偏差は最小になっていることが分かります。(微分を知っている人は、最小値を達成する
の点でリターンの標準偏差は最小になっていることが分かります。(微分を知っている人は、最小値を達成する ![]() を微分で求めてみてください。)その点から右上に行くほど、高リスク・高リターンのポートフォリオということになります。
を微分で求めてみてください。)その点から右上に行くほど、高リスク・高リターンのポートフォリオということになります。
ここまで、まずは証券が2種類しかない場合を考えました。次回からは、株式がn種類ある場合のポートフォリオを考えてみましょう。
>> 平均分散分析(6)ポートフォリオのリターンの期待値2 「証券がn個の場合」
