目次へ

>> 序，１，２，３，４，５，６，７，８，９，10，11

リスク・リターン・フロンティア２　「証券がｎ個の場合」


前々回と前回の内容をまとめます。ｎ個の株式があり、リターンの期待値が \mu = (\mu_1, \mu_2, \cdots, \mu_n)，分散共分散行列が V で与えられているとき、w = (w_1, w_2, \cdots, w_n)' というポートフォリオのリターンは

標準偏差が \sqrt{w'Vw}
期待値が \mu w

です。（\mu w は \mu_1w_1 + \mu_2w_2 + \cdots + \mu_nw_n の意味です。）


ポートフォリオをいろいろ作り、それぞれリターンの標準偏差と期待値を計算してプロットしてみましょう。たとえば最初に４つの証券があって、V が以下のように与えられているとします。

    \begin{eqnarray*}V =\left( \begin{array}{cccc}21.4 & 7.9 & 7.4 & 10.8\\7.9 & 52.3 &11.7 & 20.4\\7.4 & 11.7 & 23.9 & 12.5\\10.8 & 20.4 & 12.5 & 48.6\end{array} \right)\end{eqnarray*}


４つの証券の標準偏差は、分散（対角成分）の平方根なので、

    \begin{eqnarray*}\sigma = (4.6, 7.2, 4.9, 7.0)\end{eqnarray*}


です。また、４つの証券の期待リターンは次にように与えられているとします。

    \begin{eqnarray*}\mu = (0.64, 0.46, 1.19, 1.24)\end{eqnarray*}


横軸に標準偏差、縦軸に期待値を取って図示すれば、４つの証券は以下の赤い点で表されます（単位は％）。



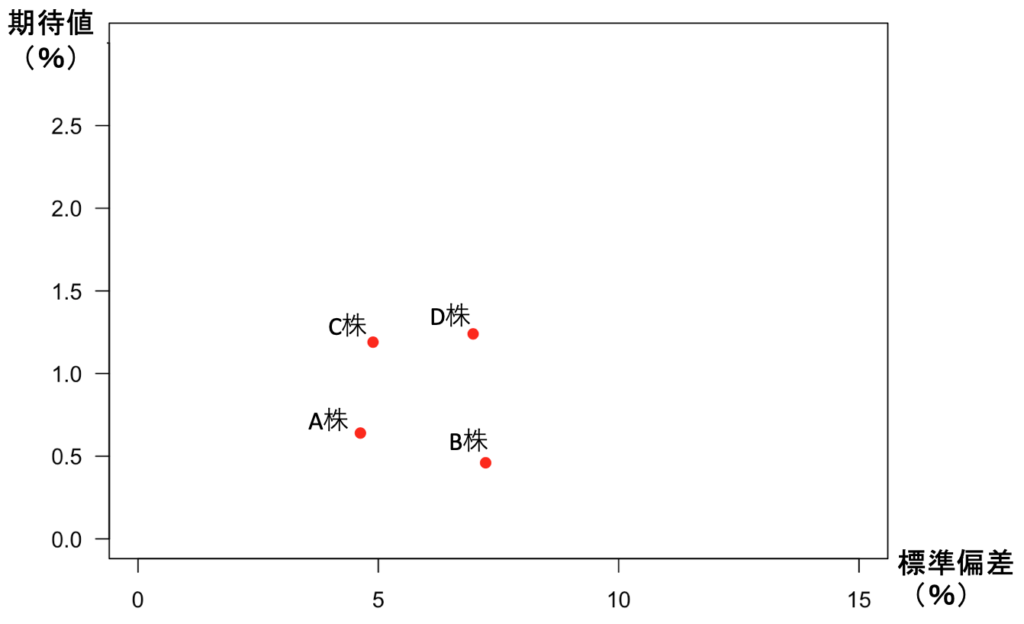
次の図では、４つの証券を組み合わせたポートフォリオをランダムに10,000通り作って、それらのリターンの標準偏差と期待値をプロットしてみました。「証券が２個の場合」では双曲線でしたが、証券が３つ以上ある場合は、もっと多様な点を達成することができます。




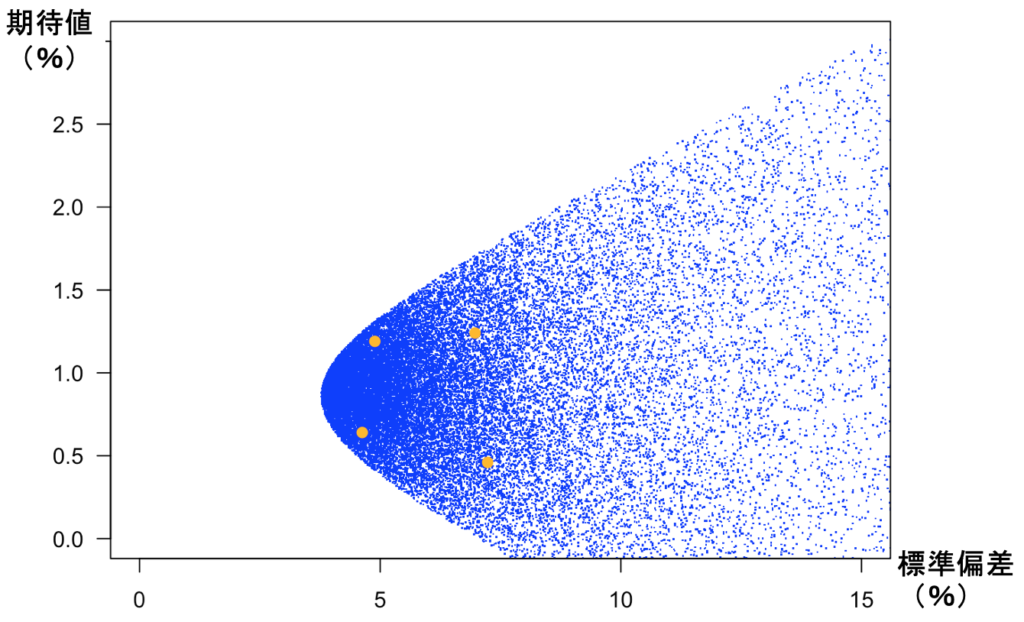
小さな点の１つ１つが、ポートフォリオを表しています。もとの４つの点から大きく離れた点は、大規模な空売りをすることで達成されています。


以下はこの散布図をエクセルで描く方法を説明した動画です。添付のエクセルファイルを使って、動画を見ながらぜひ自分で試してみてください。


これら無数の点のうち、投資家が選ぶべきはどの点でしょうか。次回はそれを考えてみましょう。

>> 平均分散分析（９）ポートフォリオ最適化１（図解編）




演習用エクセルファイルダウンロード