目次へ

>> 序，１，２，３，４，５，６，７，８，９，10，11

ポートフォリオ最適化２（定式化編）


今回は、ランダムにポートフォリオを作るのではなく、ポートフォリオを選択する問題です。ｎ種類の証券を組み合わせて、自分にとって最適なポートフォリオを選ぶ投資家の問題を、定式化してみましょう。


ｎ個の証券の期待リターンは \mu=(\mu_1, \mu_2, \cdots, \mu_n) で、分散共分散行列は V で与えられているとします。\mu と V は所与であり、投資家がどうこうすることはできません。投資家が決められるのは、各証券のウェイト w = (w_1, w_2, \cdots, w_n) です。


ポートフォリオの最適化の問題には何種類かあります。


１．分散の最小化

    \begin{eqnarray*}&& \min_{w} \;\; w'Vw\\&&\mbox{~s.t.~} \\&&\mu w \geq a\\&& \iota w =1\end{eqnarray*}



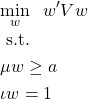
まずはポートフォリオのリスクたる分散を最小化する問題です。min は「最小化」の意味で、その右側に書かれた分散が最小化のターゲット（目的関数）です。また、minの下方に書かれた w は、w を選ぶことで最小化することを表しています。


制約は「s.t. 」に続けて書く決まりです。s.t. は subject to… （～の制約下で）の頭文字です。１つめの制約式「 \mu w \geq a 」は、最低限欲しい期待リターンを設定しています。 a が「期待リターンの下限」で、投資家が自由に決めてよい値です。小さめの a で我慢すれば、分散も小さくできますが、欲張って高い a を設定すると、分散はあまり小さくできません（“ハイリスク・ハイリターン”）。２つめの制約式は、ウェイトの合計が１になるという条件を、ベクトルの内積で表現したものです。\iota =(1,1, \cdots, 1) は１をｎ個並べたベクトルです。したがって \iota w=w_1 + w_2 + \cdots + w_n です。


２．期待リターンの最大化

    \begin{eqnarray*}&& \max_{w} \;\; \mu w\\&&\mbox{~s.t.~} \\&& w'V w \leq a\\&& \iota w =1\end{eqnarray*}


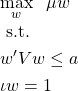
許容できるリスクを設定し、ポートフォリオの期待リターンを最大化する問題です。１つめの制約式「 w'V w \leq a 」の a が「リスクの上限」です。これも投資家が自由に決めて良い値です。大きめの a を許容できるならば、ポートフォリオの期待リターンを大きくすることができます。逆に、a を小さく設定するほど、達成できる期待リターンも小さくなってしまいます。２つめの制約式は先程と同じです。


３．期待リターンとリスクのバランスを取る

    \begin{eqnarray*}&& \max_{w} \;\; \mu w - a (w'Vw)\\&&\mbox{~s.t.~} \\&& \iota w =1\end{eqnarray*}


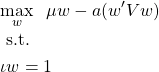
今度はポートフォリオのリターンの期待値とリスクをくっつけたものを最大化します。期待値は嬉しいもの、分散は嫌なものなので、分散の前にはマイナスの符号が付いています。ここでも a は投資家が自由に設定して良い値です。a を大きくするほど、投資家はリスクに対するペナルティーを高くしていることになります。


４．空売り制限

ここまで、w = (w_1, w_2, \cdots, w_n) の符号に制限は課しませんでした。「空売り」を許していたのです。空売りを制限する場合は、w \geq 0 という不等式制約（すなわち w_1 \geq 0 , \cdots, w_n \geq 0 というｎ本の不等式）を追加する必要があります。たとえば、空売り無しで期待リターンを最大化する問題は


    \begin{eqnarray*}&& \max_{w} \;\; \mu w\\&&\mbox{~s.t.~} \\&& w'V w \leq a\\&& \iota w =1\\&& w \geq 0\end{eqnarray*}


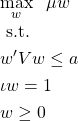
となります。


これらの問題は、複雑に見えますが、数学的には所詮「二次式」です。例えば１つめの問題を見てみると、制約式は w の一次式、目的関数は w の二次式です。この問題は、ソルバーを使って数値的に解くことができます。また、実はラグランジュ未定乗数法を使って解析的に解くこともできます。（空売り制限の不等式がない場合）


しかし、解析解を求めるのは後々の上級コースに取っておいて、次回はエクセルのソルバーを用い、数値的にポートフォリオ最適化問題を解いてみることにましょう。


>> 平均分散分析（11）ポートフォリオ最適化３（ソルバー編）