ポートフォリオ最適化1(図解編)
前回は、ランダムに様々なポートフォリオを作ってみることで、どのようなリスクとリターンの組み合わせが達成できるのかを図示してみました。今回はそれを復習しつつ、投資家の選択について考えたいと思います。
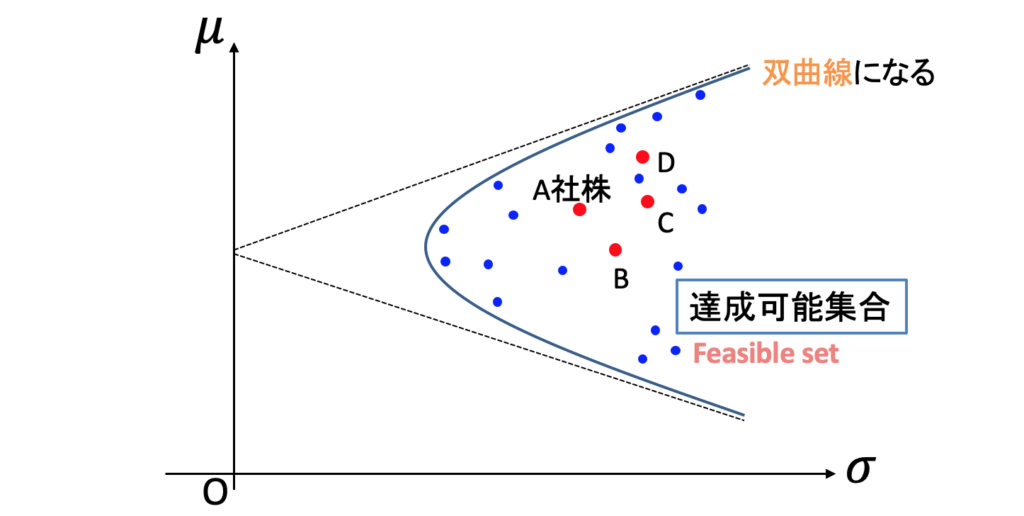
最初に4種類の株があるという設定でした。次の図の4つの点がそれを表しています。横軸がリターンの標準偏差、縦軸が期待値です。

様々なポートフォリオのリターンの標準偏差と期待値を計算して、グラフに書き足しました。青い点の1つ1つがポートフォリオです。

たくさんのポートフォリオを作って点を打っていくと、双曲線が浮かび上がります。この双曲線の内側の領域は「達成可能集合 (Feasible set)」と呼ばれます。この領域内の点であれば、4つの株を組み合わせて達成できるという意味です。
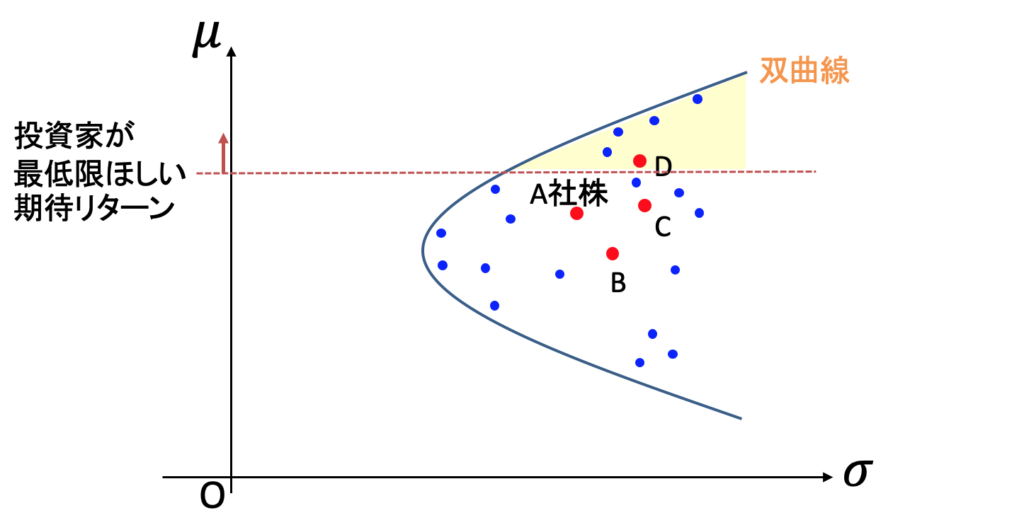
投資家にとって、ポートフォリオの期待リターンは高いほど良く、標準偏差は低いほどありがたいものです。そこで今、「最低でも◯%の期待リターンが欲しい」という投資家がいたとしましょう。するとその投資家は、次の図の黄色い領域の中から一番いい点を選ぶことになります。
標準偏差はできるだけ低い方が良いので、黄色い領域の中から投資家が選ぶ点は、次の図で「リスク最小」と記された点になります。
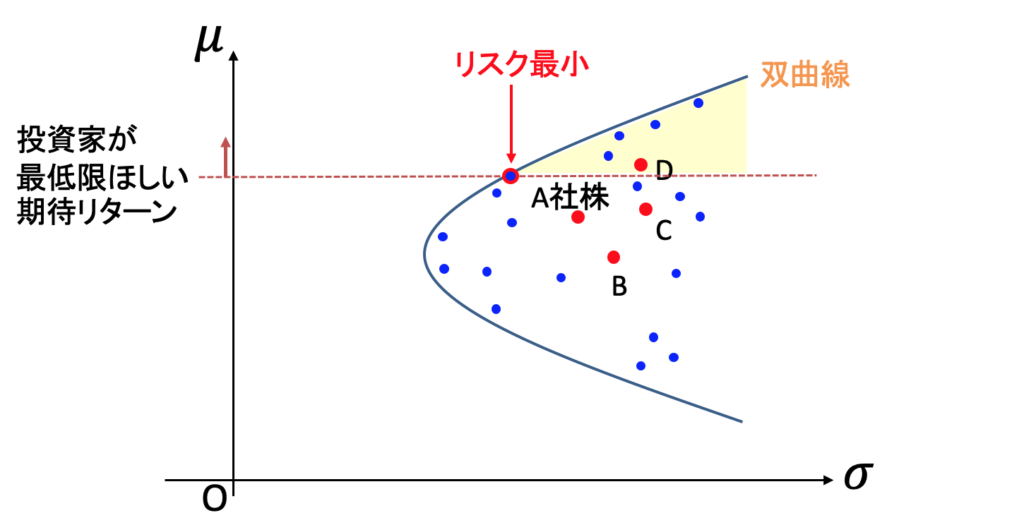
このように、おのずと達成可能集合の境界、つまり双曲線上の点が選ばれます。達成可能集合の内部の方の点を選ぶことは非効率です。
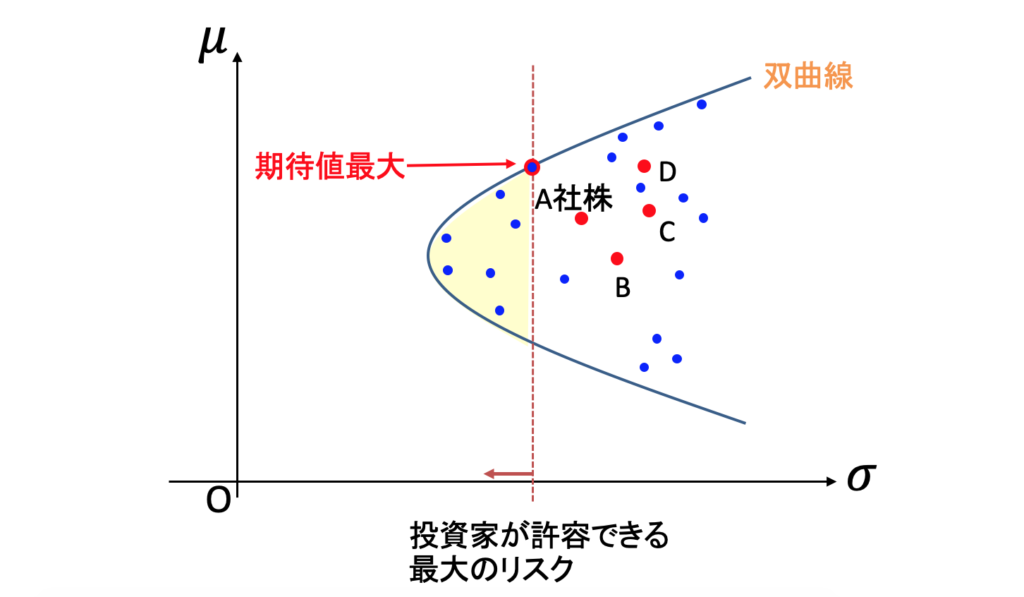
次に、投資家が「ポートフォリオのリターンの標準偏差を◯%以下に抑えたい」と考えたとしましょう。すると投資家は、以下の図の黄色い領域の中から一番いい点を選ぶことになります。
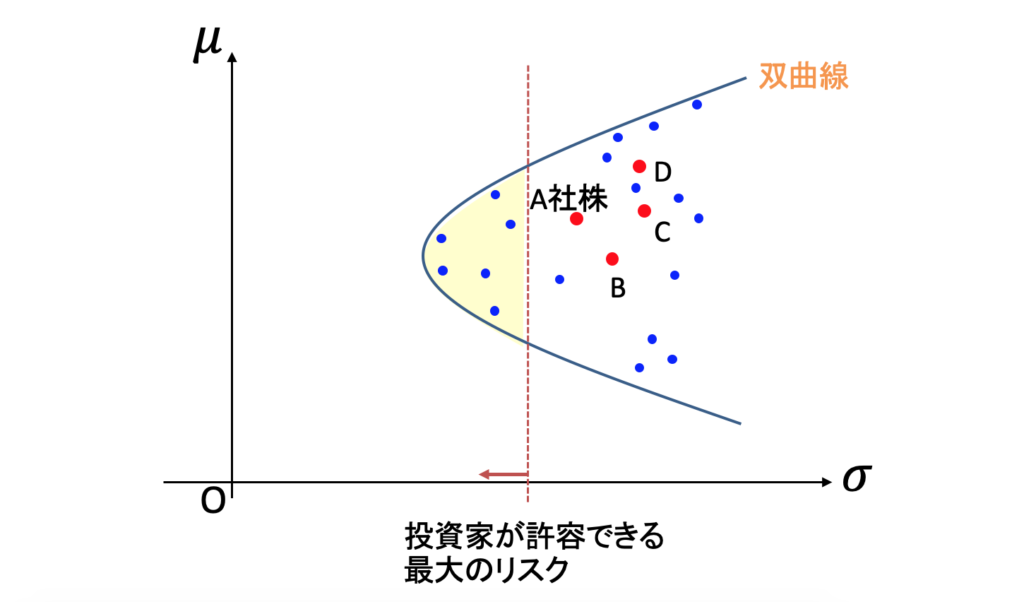
黄色い領域の範囲内で、できるだけ期待リターンを高くしようとおもったら、やはり選ばれる点は双曲線上の点になります。
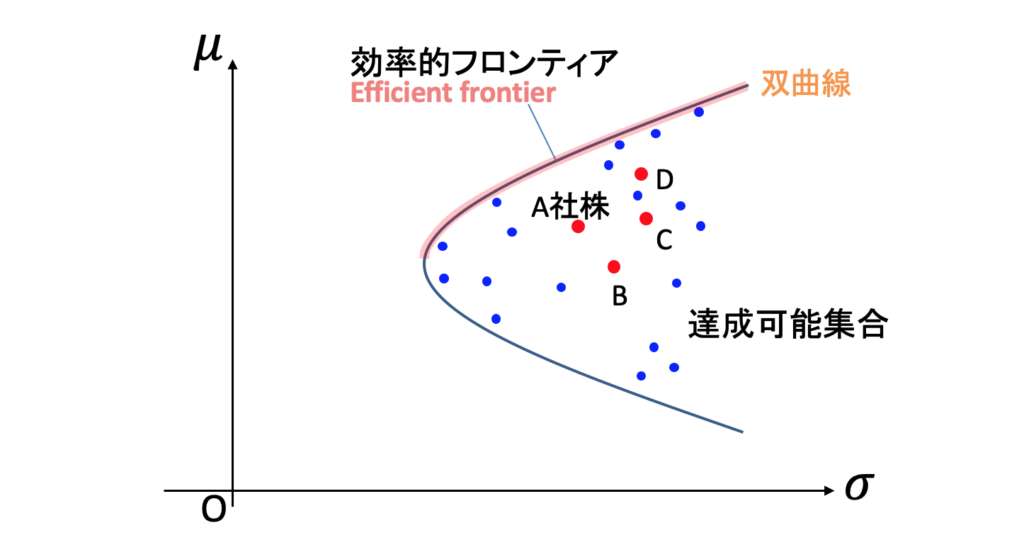
高リスク・高リターンを求める投資家であろうが、低リスク・低リターンを求める投資家であろうが、双曲線上の1点を選ぶことになります。それ以外の点を選ぶのは非効率です。こういうわけで、双曲線の上半分は「効率的フロンティア (Efficient frontier)」と呼ばれます。
次回は、こうした投資家の問題を、正式に数学的に表現してみたいと思います。
>> 平均分散分析(10)ポートフォリオ最適化2(定式化編)
