<<(1)
「線型結合」の期待値
確率変数が ![]() というように複数あるとします。このとき、これらに係数をつけてから足したものを確率変数の「線型結合」と言います。例えば
というように複数あるとします。このとき、これらに係数をつけてから足したものを確率変数の「線型結合」と言います。例えば ![]() のようなものです。(もし、
のようなものです。(もし、![]() どうしの積や2乗、つまり
どうしの積や2乗、つまり ![]() や
や ![]() があったら、線型結合とは呼べません。)
があったら、線型結合とは呼べません。)
確率変数の線型結合の期待値に関しては、次の定理が知られています。
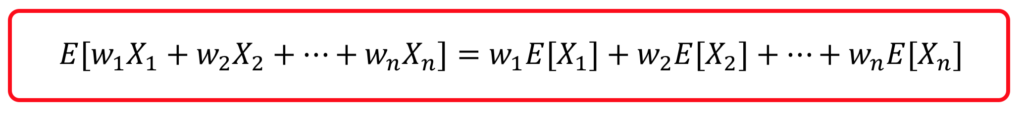
ここでは確率変数につく「係数」を ![]() で表しています。先ほどの例は、
で表しています。先ほどの例は、![]() ,
, ![]() ,
, ![]() ,
, ![]() の場合で、
の場合で、
![]()
となります。この定理は、個々の確率変数の期待値が分かれば、それらの線型結合の期待値も、自動的に分かることを表しています。
定理の式の右辺を、ベクトルの内積を使って表す方法も知っておいてください。まず、期待値はギリシア文字の
![]()
と定義すれば、
![]()
というふうに、内積で表されることになります。定理の意味は変わりません。書き表し方が変わっただけです。
この定理は、ファイナンスで、金融資産のポートフォリオの期待収益率を求めるのに応用されます。別の記事で紹介しますので、それも参照してこの公式のイメージを膨らませてくださいね。
>> 和の分散公式(1)
