労働市場論（サーチ・モデル）補論２

一次斉次な関数

全ての変数を $m$ 倍すると、関数の値も $m$ 倍になる場合、そのような関数は「一次斉次 (homogenous of degree one)」であると言います。（注：一次同次と呼ぶことも多い。）例えば

$\begin{eqnarray*}f(K, N) = A K^{\alpha} N^{1-\alpha} \end{eqnarray*}$

は、 $A$ と $\alpha$ をパラメータとすれば、 $K, N$ の一次斉次関数です。実際 $K$ と $N$ のところに $mK$ と $mN$ を代入すると、

$\begin{eqnarray*}f(mK, mN) &=& A(mK)^{\alpha} (mN)^{1-\alpha}\\&=&Am^{\alpha}K^{\alpha}m^{1-\alpha}N^{1-\alpha}\\&=&m^{\alpha}m^{1-\alpha} AK^{\alpha}N^{1-\alpha}\\&=& m AK^{\alpha}N^{1-\alpha}\\&=& m f(K, N)\end{eqnarray*}$

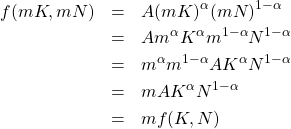
となり、確かに関数の値が元の $m$ 倍になります。この関数には「コブ・ダグラス型関数」という名前がついています。

別の例としては

$\begin{eqnarray*}g(x, y) = \frac{xy}{x+y}\end{eqnarray*}$

があります。 $x$ ， $y$ のところに $mx$ ， $my$ を代入すると

$\begin{eqnarray*}g(mx, my) &=& \frac{(mx)(my)}{(mx+my)}\\&=& \frac{m^2xy}{m(x+y)}\\&=& m \cdot \frac{xy}{x+y}\\&=& mg(x, y)\end{eqnarray*}$

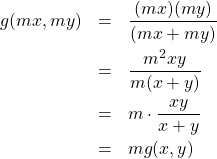
となり、関数の値は元の $g(x,y)$ の $m$ 倍になります。

経済学で一次斉次の関数が使われるのは主に「生産関数」と「マッチング関数」です。生産関数が一次斉次であると仮定することは、「資本や労働など、生産に必要な全ての要素の投入量を2倍、3倍、 $m$ 倍すれば、生産量も2倍、3倍、 $m$ 倍になる」と仮定するということです。これは妥当な仮定と言えます。

「マッチング関数」は、例えば相手を探す男性の数と女性の数を入れると、成立するカップルの数が出てくるような関数です。男性の数と女性の数がそれぞれ2倍、3倍、 $m$ 倍と増えていくと、成立するカップルの数も2倍、3倍、 $m$ 倍に増えていくというのは妥当な仮定と言えます。求職者とジョブのマッチング関数にもそのように仮定するのが普通です。「ジョブを探す労働者の数」と「求人中のジョブの数」がともに2倍、3倍、 $m$ 倍に増えていくと、人とジョブのマッチ数も2倍、3倍、 $m$ 倍に増えていくというのは妥当な仮定と言えます。

「一次斉次の関数」の定義、具体例、意味合いをしっかり言えるように、頭に入れておきましょう。