1,2,3,4,5,6,7,8,9,10,11,12,13,補1,補2,補3
「ジョブを見つける確率」と「ジョブが埋まる確率」
今回は2つの確率を定義し、サーチ・モデルの連立方程式の2~4番目の式を導出します。

失業者が1期間のあいだに就業できる確率を ![]() と置きます。例えば、もし100人のうち40人がジョブを見つけられるなら
と置きます。例えば、もし100人のうち40人がジョブを見つけられるなら ![]() は0.4です。
は0.4です。![]() は「ジョブを見つける確率 (Job-finding probability)」と呼ばれます。
は「ジョブを見つける確率 (Job-finding probability)」と呼ばれます。
一方、欠員状態のジョブ(求人中のジョブ)が1期間のあいだに労働者とマッチできる確率を ![]() と置きます。もし100個のジョブのうち、20個が労働者とマッチできるなら、
と置きます。もし100個のジョブのうち、20個が労働者とマッチできるなら、![]() は0.2です。
は0.2です。![]() は「ジョブが埋まる確率 (Job-filling probability)」と呼ばれます。
は「ジョブが埋まる確率 (Job-filling probability)」と呼ばれます。
今回は、この ![]() と
と ![]() を、前回紹介したマッチング関数から導出します。マッチング関数の仮定により、失業者の数が
を、前回紹介したマッチング関数から導出します。マッチング関数の仮定により、失業者の数が ![]() ,求人中のジョブの数が
,求人中のジョブの数が ![]() のとき、1期間中にマッチする労働者とジョブのペアの数は
のとき、1期間中にマッチする労働者とジョブのペアの数は ![]() です。このとき「ジョブを見つける確率」
です。このとき「ジョブを見つける確率」 ![]() はいくつでしょうか。
はいくつでしょうか。
失業者 ![]() 人のうち
人のうち ![]() 人がジョブとマッチするので、マッチできる人の割合である
人がジョブとマッチするので、マッチできる人の割合である ![]() が「ジョブを見つける確率」です。シミュレーションのためには
が「ジョブを見つける確率」です。シミュレーションのためには ![]() を具体的に仮定する必要があるので、マクロ経済学でよく用いられるコブ・ダグラス型関数(
を具体的に仮定する必要があるので、マクロ経済学でよく用いられるコブ・ダグラス型関数(![]() )を使うことにします。そうすると、
)を使うことにします。そうすると、
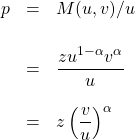
となります。
次に、「ジョブが埋まる確率」
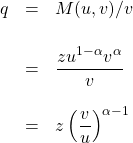
となります。
「ジョブを見つける確率」も「ジョブが埋まる確率」も、
有効求人倍率
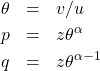
となります。これがイントロで示した10本の式のうちの3本です。
次回は「労働者の生涯所得」と「ジョブの現在価値」を考えます。
>> 労働市場論(サーチ・モデル)(7)「労働者の生涯所得」と「ジョブの現在価値」
