１，２，３，４，５，６，７，８，９，10，11，12，13，補1，補2，補3
数値シミュレーション１ 賃金と失業
今回は、コンピューターを使ってサーチ・モデルを数値的に解いた結果を紹介したいと思います。外生変数（“パラメータ”）を１つ選び、その値を変化させながら、解（＝均衡）がどのように変化するかを見たいと思います。（そのようなエクササイズを、経済学では「比較静学 (comparative statics) 」と言います。）
今回は、労働者の交渉力を表す 
を変化させてみましょう。労働者の交渉力は、労働法制によって比較的容易に影響を与えられるパラメータです。 の値を0から1まで変化させ、均衡がどのように変化するかを調べます。
以下では、 以外のパラメータの値は 
，
，
，
，
，
，
と設定しました (注1)。図が表示するのは３つの内生変数（賃金 
，ジョブを見つける確率 
，失業率 
）です。 の値が上がるにしたがって、各内生変数の値が上がるか下がるかに注目してください。
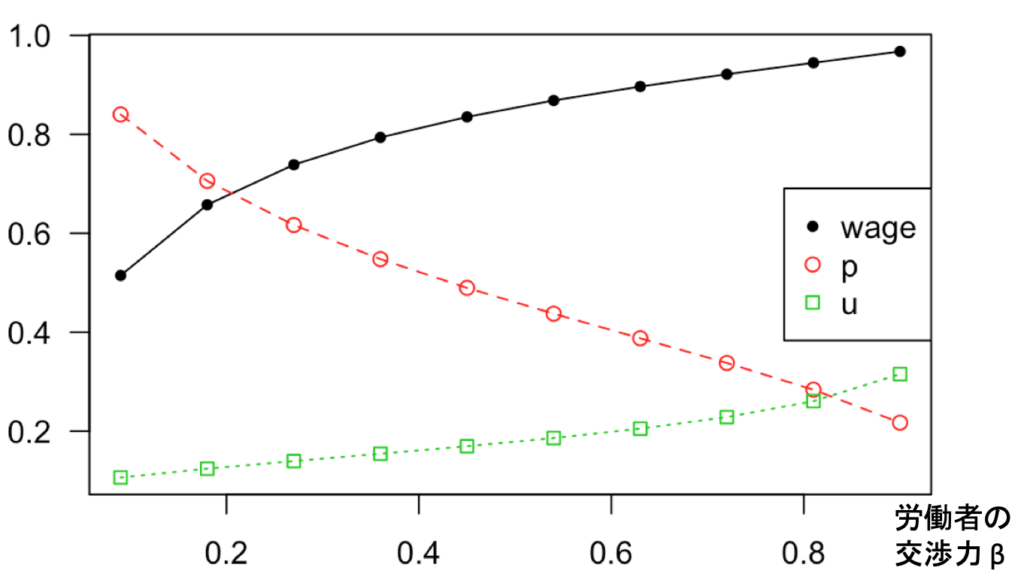
まず、賃金を見てみましょう。wageと表示されている黒い線が賃金です。 が１に近づくほど、賃金が高くなっていることが分かります。労働者の交渉力が上がるほど賃金が高くなるのは、直観に合った結果です。
次に、「ジョブを見つける確率」を見てみましょう。 と表示されている赤い線がそうです。 が１に近くほど、失業者がジョブを見つける確率は低くなっています。これも直観に合った結果です。労働者の交渉力が高いほど賃金が高くなるため、企業の求人数が抑制されるからです。失業者がジョブを見つけられる確率が下がる結果として、失業率（ と表示されている緑の線）は上昇しています。
労働者にとっては、賃金もジョブを見つけられる確率も大事です。そこで次回は、労働者全体の厚生を見ながら、労働者の賃金交渉力はどれくらい高いのがちょうど良いのかをシミュレーションしてみましょう。
>> 労働市場論（サーチ・モデル）（13）数値シミュレーション２ 厚生
注1）これらのパラメータの値は、本来は根拠をもって選ぶべきで、この作業を「カリブレーション (calibration)」と言います。今日はカリブレーションは行わず、パラメータの値は適当に選んでいます。ですので、内生変数の大きさじたいは気にせず、 の値が上がるにしたがって上がるか下がるかだけに注目してください。