労働市場論（サーチ・モデル）（11）

モデルを解く

このシリーズで勉強している基本のサーチ・モデルは、10変数・10式の連立方程式で表されました。

今回は、解き方です。変数の消去によって、2変数・2式まで減らすテクニックを紹介します。サーチ・モデルを応用した多くの論文で使われるテクニックです。（計算過程を不要とする人は、この回は飛ばして先に進むことができます。）

まず手始めに、(10)式（ $V_0=0$ ）を他の式に代入します。すると(9)式（賃金決定式）は

$\begin{eqnarray*}W_1-W_0 = \beta(W_1- W_0 + V_1)\end{eqnarray*}$

となります。

ここで、 $S\equiv W_1-W_0+V_1$ と置くと、

$\begin{eqnarray*}&&W_1-W_0 = \beta S\\\\&&V_1=(1-\beta)S\end{eqnarray*}$

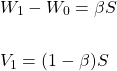
が出てきます（上の式から下の式は導ける）。これらの式はあとで用います。

次に、連立方程式の(5)・(6)式と、 $V_0=0$ を代入した(8)式を、合体させることを考えます。

$\begin{eqnarray*}W_0 &=& b + \frac{1}{1+r}\left((1-p)W_0 + pW_1\right)\\\\W_1 &=& w + \frac{1}{1+r}\left(\delta W_0 + (1-\delta) W_1\right)\\\\V_1 &=& y-w + \frac{1}{1+r} (1-\delta) V_1\end{eqnarray*}$

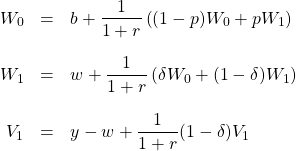
２つめと３つめの式を足し、１つめの式を引くと、

$\begin{eqnarray*}W_1-W_0+V_1 = y-b + \frac{1}{1+r} \left\{ (1-\delta) (V_1+W_1-W_0) - p(W_1-W_0) \right\}\end{eqnarray*}$

です。

ここで再び $S= W_1-W_0+V_1$ と置き、上記の $W_1-W_0=\beta S$ も使い、さらに(2)式で $p$ を消去すれば、

$\begin{eqnarray*}S = y-b + \frac{1}{1+r} \{ (1-\delta)S - z\theta^\alpha\beta S\}\end{eqnarray*}$

となります。これが導きたい２本の式のうちの１つ目です。 $S$ と $\theta$ だけの式であることを意識しましょう。

一方、連立方程式の(7)式は

$\begin{eqnarray*}V_0 = -k + \frac{1}{1+r} \left\{(1-q)V_0 + qV_1\right\}\end{eqnarray*}$

ですが、まず $V_0=0$ を代入し、次に上述の $V_1=(1-\beta)S$ で $V_1$ を消去し、さらに(3)式で $q$ も消去してしまえば

$\begin{eqnarray*}0 = -k + \frac{1}{1+r} z \theta^{\alpha-1} (1-\beta) S\end{eqnarray*}$

です。これが導きたかった２つ目の式です。これも $S$ と $\theta$ だけの式です。

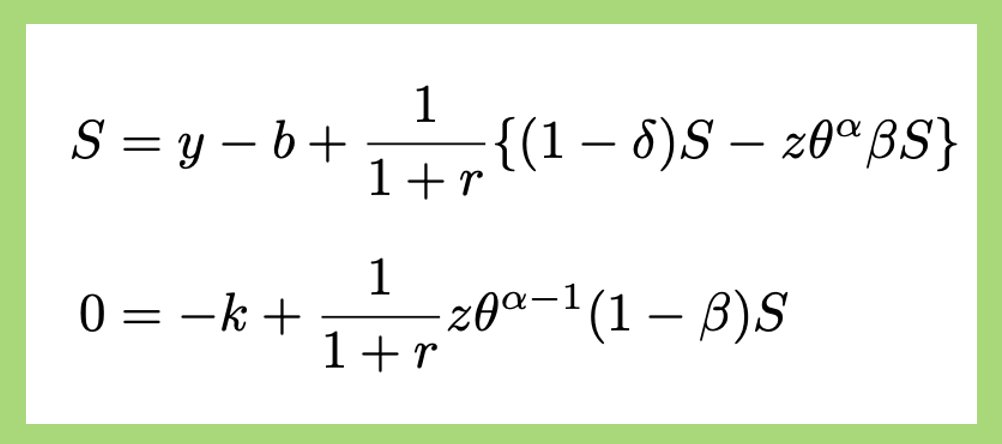
以上をまとめると、 $S$ ， $\theta$ 　という２変数のみの式が、２本だけあることになります。（ここからさらに1変数1式にすることも容易です。）

式の数がかなり減ったので、外生変数 $(y, b, r, \delta, z, \alpha, \beta, k)$ の値を全て与えれば、 $S$ と $\theta$ の値をコンピューターで簡単に求められます。

そうしていったん $\theta$ が求まれば、(2)式から $p$ ，(3)式から $q$ が求まり、 $p$ が求まれば(1)式より $u$ も求まります。また、(4)式より $\theta$ と $u$ から、 $v$ も求まります。一方、いったん $S$ が求まれば、 $V_1=(1-\beta)S$ より $V_1$ が求まり、 $V_1$ が求まれば(8)式で $w$ が定まります。一方、 $W_1-W_0 = \beta S$ より $W_1-W_0$ も求まり、 $W_1-W_0$ が求まれば(5)式によって $W_0$ が求まります。 $W_1-W_0$ と $W_0$ が求まったので $W_1$ も求まります。

次回はコンピュータを用いて解いた結果を紹介したいと思います。

>> 労働市場論（サーチ・モデル）（12）数値シミュレーション１　賃金と失業