１，２，３，４，５，６，７，８，９，10，11，12，13，補1，補2，補3
交渉力が賃金を決める
今回はサーチ・モデルの９本目の式、賃金の決定に関わる式です。
賃金 
はどう決まるか。「神の見えざる手」に頼れないことは第１回に話しました。ではどうするかというと、ここにもサーチ・モデルのうまいアイディアがあります。
まずマッチが生み出す総余剰というものを考えます。前回説明したように、労働者の生涯所得は、失業中であれば 
，就業中であれば 
ですから、労働者にとってマッチすることの恩恵は、差額の 
です。
一方ジョブの現在価値は、充足状態であれば 
，欠員状態であれば 
なので、ジョブが労働者とマッチすることの恩恵は、差額の 
です。したがって、両者の合計 
が、マッチによって労働者と企業が得る恩恵の合計、つまり「総余剰 (surplus)」ということになります。
サーチ・モデルは、マッチの総余剰を労働者と企業が 
の比で取り合うと仮定します。すなわち
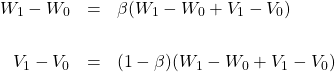
です。上の式がサーチ・モデルの連立方程式の9番目の式です。下の式は上の式から出てくる（
から上の式を引けば良い）ので、連立方程式には加えません。この式じたいには賃金
は出てきませんが、実はこの式が間接的に賃金を決定します。サーチ・モデルの式の６・８番目を見ると、賃金 は や に影響を与えることが分かります。だから、労働者と企業それぞれが得る恩恵の比を 
と固定すると、逆に賃金の方が決まってしまうというトリックになっています。次回は企業の求人数
がどのように決まるかを考えてみましょう。>> 労働市場論（サーチ・モデル）（９）参入のゼロ利潤条件