労働市場論（サーチ・モデル）（５）

マッチング関数

今回は、サーチ・モデルを構成する数々のアイディアの中で、最も重要と言っても過言ではない「マッチング関数 (matching function)」について説明します。

マッチング関数は、求職者数と求人数を入れると、マッチ（結ばれた労働者とジョブのペア）の数が出てくる関数です。基本のサーチ・モデルでは「求職者＝失業者」なので、失業者数を $u$ ，求人数を $v$ として、マッチング関数を $M(u, v)$ のように表します。例えば「0.2万人の失業者がいて、0.5万件の求人があるときは、 ◯◯万組のマッチが生まれる」といったことを教えてくれる関数です。

$M(u, v)$ は、 $u$ と $v$ のそれぞれに関して増加関数であると仮定されます。求職者や求人が多いほど、成立するマッチの数も多いという意味ですが、これは自然な仮定でしょう。

また、通常 $M(u, v)$ は「一次斉次 (homogenous of degree one)」であると仮定されます。これは、 $u$ と $v$ が同時に 2倍，3倍， $m$ 倍になった場合は、成立するマッチの数も2倍，3倍， $m$ 倍になるという仮定です。

一次斉次の関数の典型例は、マクロ経済学で最も頻繁に使われる「コブ・ダグラス型」です。（なのでこのシリーズでもマッチング関数としてコブ・ダグラス型を使います。）コブ・ダグラス型は、

$\begin{eqnarray*}M(u, v) = z u^{1-\alpha} v^{\alpha}\end{eqnarray*}$

と表されます。ここで $z$ は正の定数であり、べき数 $\alpha$ は0と1の間の定数です。この関数が一次斉次であることを確めるには、 $u$ ， $v$ の双方を $m$ 倍してみればよいです。

$\begin{eqnarray*}M(mu, mv) &=& z (mu)^{1-\alpha} (mv)^{\alpha}\\&=& zm^{1-\alpha}u^{1-\alpha}m^{\alpha}v^{\alpha}\\&=& m^{1-\alpha}m^{\alpha}zu^{1-\alpha}v^{\alpha}\\&=& m^{1-\alpha+\alpha} zu^{1-\alpha} v^{\alpha}\\&=& mzu^{1-\alpha} v^{\alpha}\\&=& mM(u,v)\end{eqnarray*}$

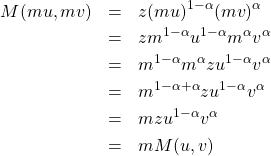
となり、確かに関数の値がもとの $m$ 倍になります。

今日の内容を要約すると、「マッチング関数とは、失業者数 $u$ と求人数 $v$ を入れるとマッチ数が出てくる関数で、増加関数で、かつ一次斉次と仮定される」です。

次回はこのマッチング関数を元に、サーチ・モデルの連立方程式の、２〜４番目の式を導出します。

>> 労働市場論（サーチ・モデル）（６）「ジョブを見つける確率」と「ジョブが埋まる確率」