1,2,3,4,5,6,7,8,9,10,11,12,13,補1,補2,補3
舞台設定
まずは、サーチ・モデルの世界の舞台設定を説明します。視覚的なイメージを持つことを心がけましょう。
時間が ![]() 1,2,3,
1,2,3,![]() と流れていきます。サーチ・モデルの世界にはたくさんの労働者がいます。労働者の人口は1に基準化します。(さしあたり1万人とか、1億人とか、大きい数字をイメージしてください。)
と流れていきます。サーチ・モデルの世界にはたくさんの労働者がいます。労働者の人口は1に基準化します。(さしあたり1万人とか、1億人とか、大きい数字をイメージしてください。)
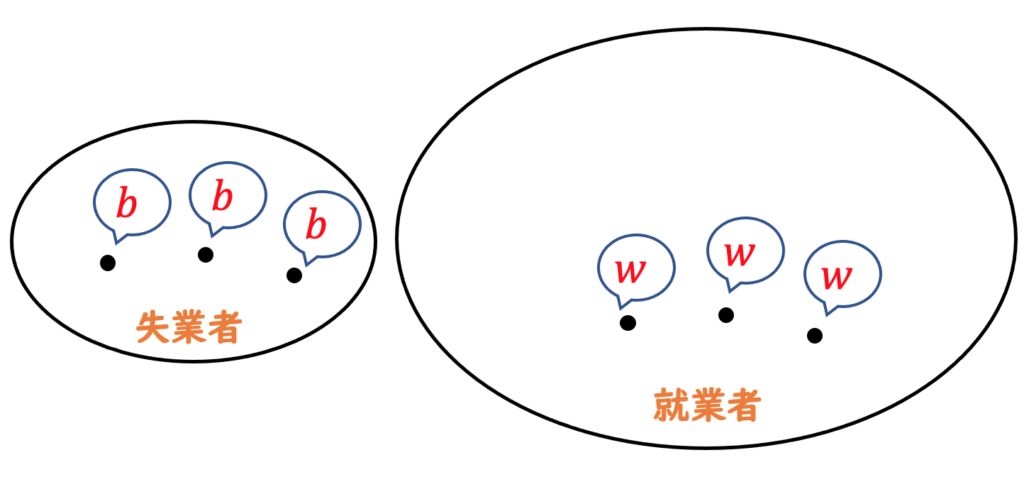
各時点において労働者は、就業中か失業中かのどちらかです。就業者は賃金 ![]() を受け取り、失業者は失業便益
を受け取り、失業者は失業便益 ![]() を得ます(失業給付金、家事による節約、等々)。ここでは
を得ます(失業給付金、家事による節約、等々)。ここでは ![]() ,すなわち就業によって得られる賃金の方が高いと仮定します。
,すなわち就業によって得られる賃金の方が高いと仮定します。
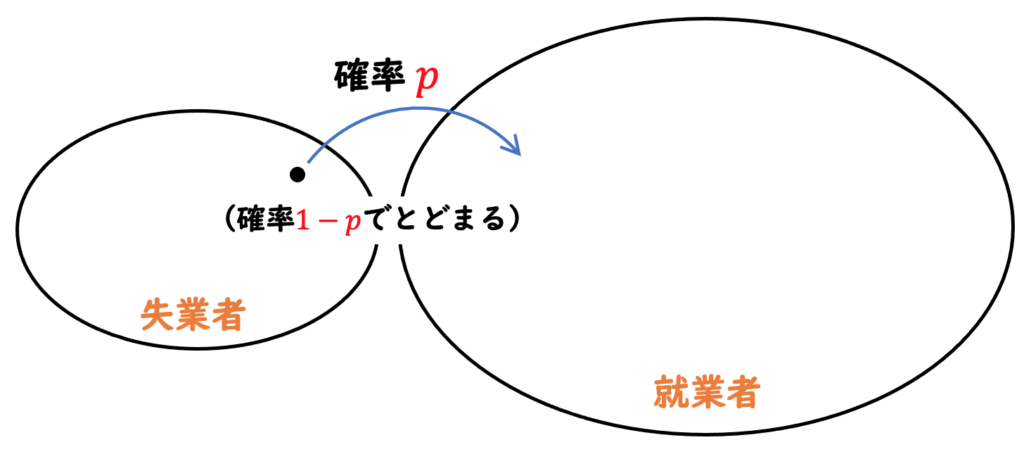
失業者は、確率 ![]() で期間中にジョブを見つけて就業者となるか、確率
で期間中にジョブを見つけて就業者となるか、確率 ![]() で失業したままかです。
で失業したままかです。![]() は「ジョブを見つける確率 (job-finding probability)」と呼ばれます。
は「ジョブを見つける確率 (job-finding probability)」と呼ばれます。
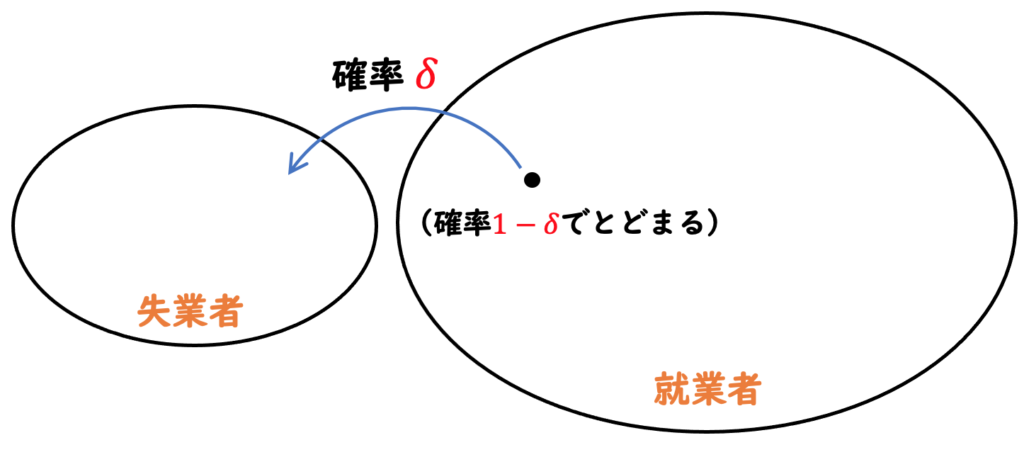
一方、就業者は、期間中に確率 ![]() でジョブと離れて失業者となるか、確率
でジョブと離れて失業者となるか、確率 ![]() でジョブとのマッチを維持するかです。転職のためにジョブを辞めるケースは考えません。
でジョブとのマッチを維持するかです。転職のためにジョブを辞めるケースは考えません。![]() は分裂確率 (separation probability) と呼ばれます。
は分裂確率 (separation probability) と呼ばれます。
次にジョブの方です。「ジョブ」の単位は「1ジョブ=1人」とします。1つのジョブが2人の労働者を雇ったり、1人で2つのジョブを掛け持ちしたりすることはありません。各ジョブは以下の3つのうちのいずれかの状態だとします。
- 雇っていないし、求人もしていない(“idle”,「休止状態」)
- 雇っていないが、求人している(“vacant”,「欠員状態」)
- 1人雇っている(“filled”,「充足状態」)
休止状態のジョブと欠員状態のジョブをまとめて「埋まっていないジョブ」と呼ぶこともあります。
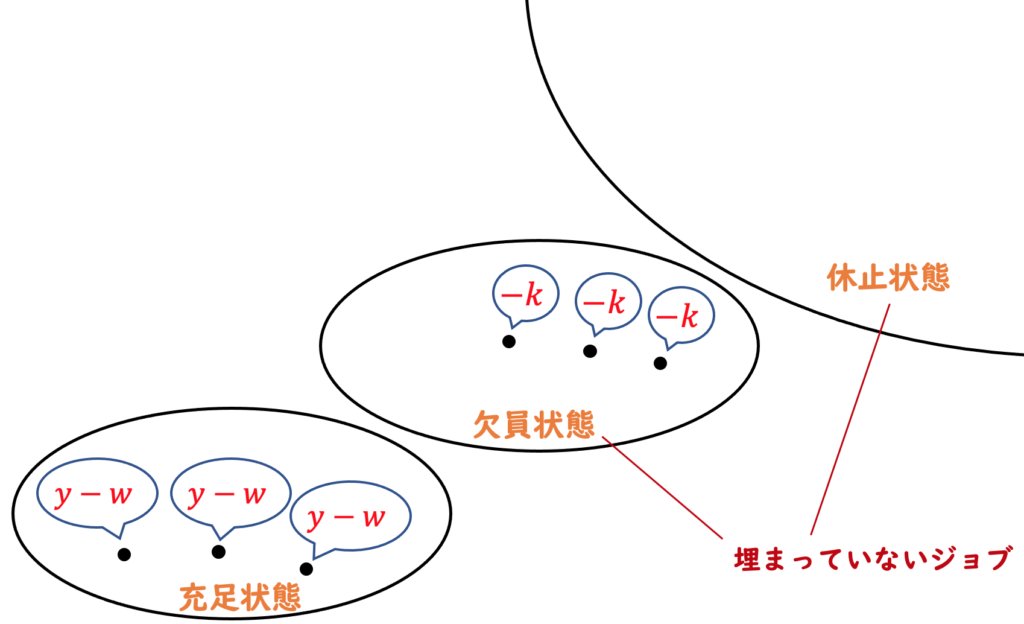
休止状態のジョブは何もしません。欠員状態のジョブは、「求人・採用活動のコスト」 ![]() を毎期支払う必要があります。一方、充足状態のジョブは毎期
を毎期支払う必要があります。一方、充足状態のジョブは毎期 ![]() 円を売上げ、労働者に
円を売上げ、労働者に ![]() 円の賃金を支払った残りの
円の賃金を支払った残りの ![]() 円を利益とします。
円を利益とします。
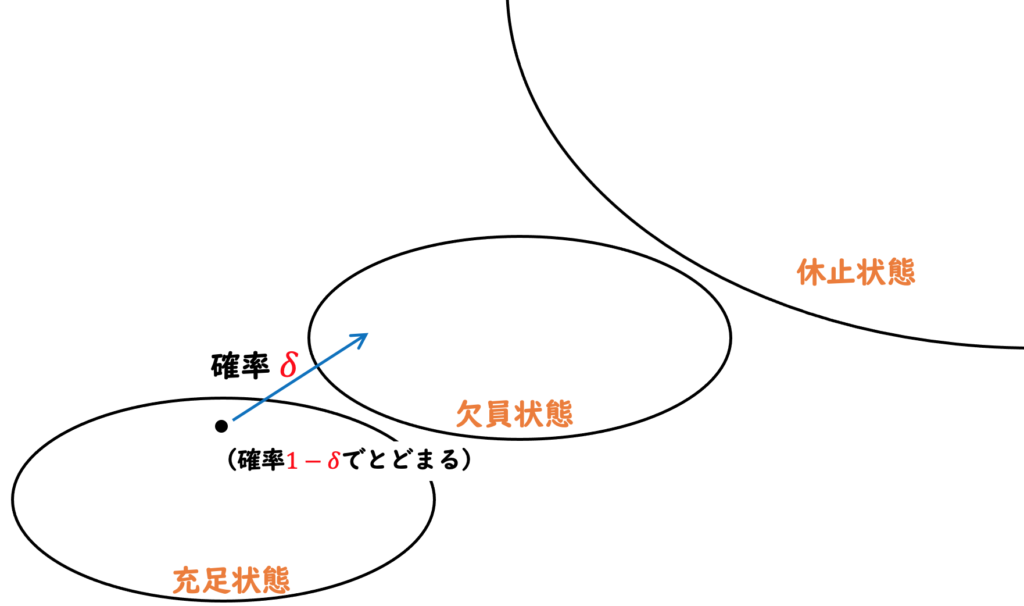
欠員状態のジョブは、期間中に確率 ![]() で労働者とマッチして充足状態となるか、確率
で労働者とマッチして充足状態となるか、確率 ![]() で欠員状態のままかです。
で欠員状態のままかです。
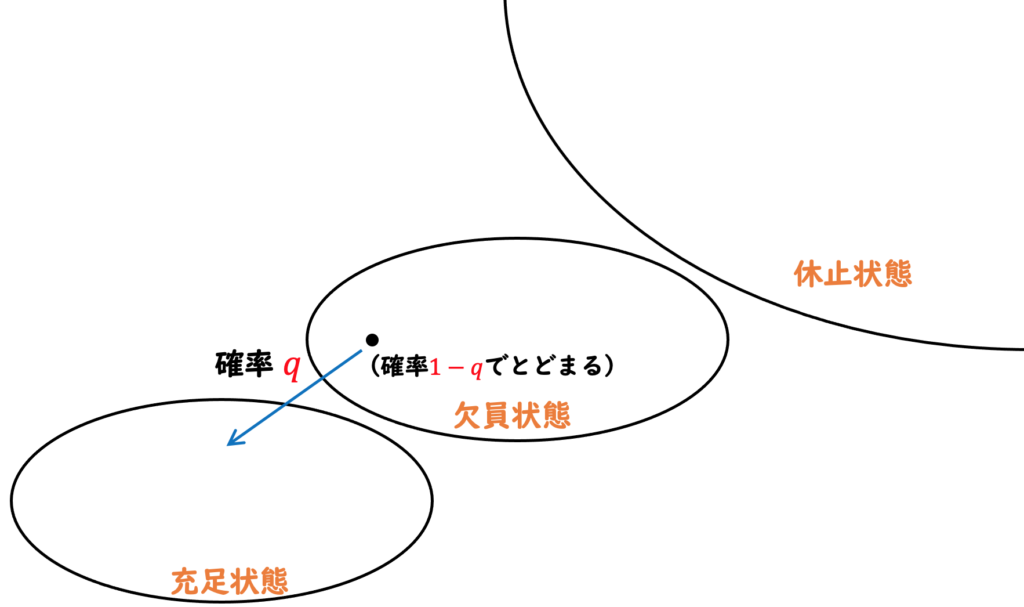
充足状態のジョブは、確率 ![]() で労働者と別れて欠員状態となるか、確率
で労働者と別れて欠員状態となるか、確率 ![]() で労働者とのマッチを維持するかです。
で労働者とのマッチを維持するかです。![]() は労働者の所でも出てきた分裂確率です。
は労働者の所でも出てきた分裂確率です。
たくさんの労働者とジョブが、毎期くっついたり離れたりしながら、それぞれの状態に応じて受け取るべきものを受け取っている(あるいは支払っている)ところをイメージできるようになったでしょうか。
次回は、この世界において失業率がどう変遷していくかを説明します。
>> 労働市場論(サーチ・モデル)(4)失業率の変遷式
