1,2,3,4,5,6,7,8,9,10,11,12,13,補1,補2,補3
数値シミュレーション2 厚生
前回のシミュレーションでは、労働者の賃金交渉力 ![]() を変化させました。結果は以下にまとめられます。
を変化させました。結果は以下にまとめられます。
- ・
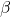 が低いと、賃金も失業率も低め
が低いと、賃金も失業率も低め - ・
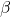 が高いと、賃金も失業率も高め
が高いと、賃金も失業率も高め
すなわち、労働者にとって、![]() は単純に高ければ良いというわけではありませんでした。では、労働者の賃金交渉力はどれくらいが望ましいのでしょうか。それを判断するには、「労働者全体の厚生」を計算する必要があります。
は単純に高ければ良いというわけではありませんでした。では、労働者の賃金交渉力はどれくらいが望ましいのでしょうか。それを判断するには、「労働者全体の厚生」を計算する必要があります。
経済学において「厚生 (welfare)」とは、全員の利得を合算したもので、いわばその経済の良し悪しのバロメーターです。サーチ・モデルの労働者の利得は、生涯所得です。生涯所得は、失業中の人が ![]() ,就業中の人が
,就業中の人が ![]() でした。人口は失業者と就業者がそれぞれ
でした。人口は失業者と就業者がそれぞれ ![]() と
と ![]() なので、全員の生涯所得を合計したものは
なので、全員の生涯所得を合計したものは
![]()
です。これが「労働者全体の厚生」の指標となります。労働者の交渉力
「労働者全体の厚生」は労働者のみを考えた指標です。これとは別に、企業のことも考慮した「経済全体の厚生」という指標もあります。こちらは、労働者の利得に、企業の利得も合わせた、経済の良し悪しの指標です。
企業の利得は、利益です。企業が生み出す利益の現在価値は、充足状態のジョブが
![]()
となります(注1)。(
以下が計算結果です(注2)。横軸が
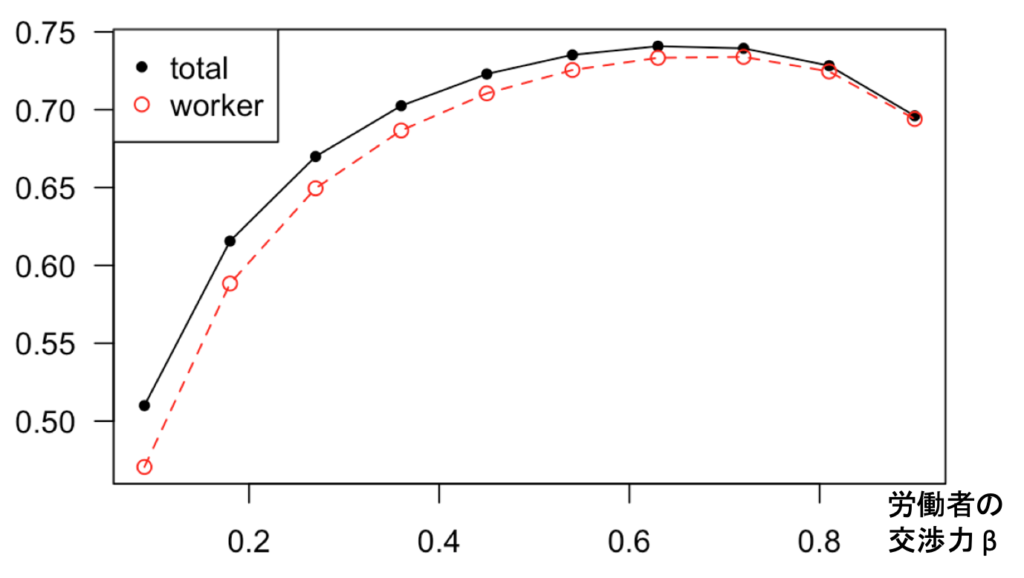
労働者の賃金交渉力が高過ぎも低過ぎもしないとき(図では0.7くらい)に、「労働者の厚生」が最も高いという結果になりました。先述したように、これは賃金と失業率のバランスを取っているためです。「社会全体の厚生」もグラフはほとんど変わりません(注3)。最大になるのは ![]() が高過ぎも低過ぎもしないとき(図では0.65くらい)であることが分かります(注4)。
が高過ぎも低過ぎもしないとき(図では0.65くらい)であることが分かります(注4)。
いかがでしたか。これらのシミュレーションの結果は、そのまま現実の政策に当てはめられるものではありません。それでも、変数間の複雑な関係を可視化し、私たちの理解を深めてくれます。それが、厳密な議論とモデルのさらなる改良の、出発点となってくれるのです。(終わり)
注1)実はこれは「毎期 ![]() を生み出すことの割引現在価値」に等しくなることが数式的に証明できます。
を生み出すことの割引現在価値」に等しくなることが数式的に証明できます。
注2)正確には、![]() を乗じたもの(=割賦価値)をグラフ化しています。
を乗じたもの(=割賦価値)をグラフ化しています。
注3)これは、このモデルにおける企業が設備などの資本を保有せず、労働力だけに頼って生産しているためです。
注4)理論的には ![]() のときに社会全体の厚生が最大になることが、A. ホシウスによって証明されました。あまり直観的でない不思議な結果ですが、これは企業の採用コストに関わっています。
のときに社会全体の厚生が最大になることが、A. ホシウスによって証明されました。あまり直観的でない不思議な結果ですが、これは企業の採用コストに関わっています。![]() が低いと、企業は採用活動をし過ぎて、採用のコストを出費し過ぎる。逆に
が低いと、企業は採用活動をし過ぎて、採用のコストを出費し過ぎる。逆に ![]() が高すぎると、企業は採用活動をしなさすぎるのです。
が高すぎると、企業は採用活動をしなさすぎるのです。
