>> 序,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18
ベルヌーイ分布以外の「二者択一」分布
ベルヌーイ分布は「0か1か」の二者択一の確率分布です。一方、100万円もらえるか失うかの賭けは「100か、![]() か」であって「0か1か」ではないので、厳密にはベルヌーイ分布ではありません。しかし、このような二者択一の確率変数の期待値や分散は、ベルヌーイ分布の期待値や分散を利用することで、簡単に求めることができます。それをこれから説明しましょう。今、
か」であって「0か1か」ではないので、厳密にはベルヌーイ分布ではありません。しかし、このような二者択一の確率変数の期待値や分散は、ベルヌーイ分布の期待値や分散を利用することで、簡単に求めることができます。それをこれから説明しましょう。今、
確率 ![]() で
で ![]()
確率 ![]() で
で ![]()
が実現する確率分布を考えましょう。そのような分布にしたがう確率変数を ![]() ,ベルヌーイ分布にしたがう確率変数を
,ベルヌーイ分布にしたがう確率変数を ![]() と表すことにします。以下の表は
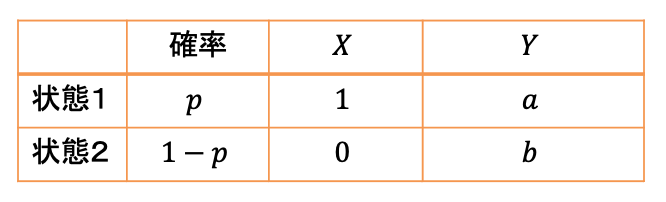
と表すことにします。以下の表は ![]() と
と ![]() の関係をまとめています。
の関係をまとめています。
ベルヌーイ分布の期待値と分散は、前回求めたように ![]() ,
,![]() です。では
です。では ![]() の期待値と分散はどうなるでしょうか。ここで有用となるのは、上述の
の期待値と分散はどうなるでしょうか。ここで有用となるのは、上述の ![]() が
が ![]() の式で表せるという事実です。その式は
の式で表せるという事実です。その式は ![]() というものです。
というものです。![]() のときに
のときに ![]() で、
で、![]() のときに
のときに ![]() だからです。
だからです。
この事実を用いて、![]() の期待値、分散、標準偏差を求めましょう。まず期待値は
の期待値、分散、標準偏差を求めましょう。まず期待値は
![Rendered by QuickLaTeX.com \begin{eqnarray*}E[Y] &=& E[(a-b)X+b]\\&=& (a-b)E[X] + b\\&=& (a-b)p + b \\&=& pa + (1-p)b\end{eqnarray*}](https://blog-study-economics.com/wp-content/ql-cache/quicklatex.com-b65393d9f2c29d422276070770f0b70c_l3.png)
1つめのイコールは
分散は、分散公式を用いれば
![Rendered by QuickLaTeX.com \begin{eqnarray*}\mbox{Var}[(a-b)X+b] &=& \mbox{Var}[(a-b)X]\\&=& (a-b)^2\mbox{Var}[X]\\&=& (a-b)^2 p(1-p)\end{eqnarray*}](https://blog-study-economics.com/wp-content/ql-cache/quicklatex.com-59a1a012010bc06756c49ddddf3d4757_l3.png)
です。1つめのイコールは、「定数項は分散には無関係」という事実を用いています。2つめのイコールは係数が2乗して分散の外に出ることを用いています。3つめのイコールは、ベルヌーイ分布の分散が
標準偏差は分散の平方根ですから、
ここまで、離散型の確率分布の代表例の1つめ「ベルヌーイ分布」とその派生形を勉強してきました。次回は「ベルヌーイ試行」の概念を知り、離散型の確率分布の2つめ「二項分布」に進みましょう。
今日のポイント![]() か
か ![]() かという二者択一の分布の期待値と分散は、ベルヌーイ分布の期待値と分散を利用して求めることができる。
かという二者択一の分布の期待値と分散は、ベルヌーイ分布の期待値と分散を利用して求めることができる。

