>> 序,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18
幾何分布の期待値
幾何分布の期待値を計算しましょう。期待値は、対応する実現値と確率の積の和でした。すなわち
![]()
![]()
です。{ } の中は、等差数列
![]()
と表したうえで、この両辺に
![]()
を辺々引くというものです。すると
![]()
というふうに、右辺は初項が
![]()
これより、
分散の計算は少し複雑なので、補論にしたいと思います。次回は確率のモデル化という話です。
>> 確率分布(離散型)(12)確率のモデル化
注1:
教科書によっては ![]() と表しているため、期待値の “公式” が
と表しているため、期待値の “公式” が ![]() となっていますが、これは単なる表記の違いです。
となっていますが、これは単なる表記の違いです。
補論:幾何分布の分散
分散を計算するには ![]() の公式を使うべく、
の公式を使うべく、![]() の期待値を求める。すなわち
の期待値を求める。すなわち
確率 ![]() で
で![]()
確率 ![]() で
で![]()
確率 ![]() で
で![]()
確率 ![]() で
で![]()
![]()
確率 ![]() で
で![]()
![]()
という分布の期待値である。これは
![]()
となるので
![]()
を求める必要がある。ここから
![]()
を辺々引けば
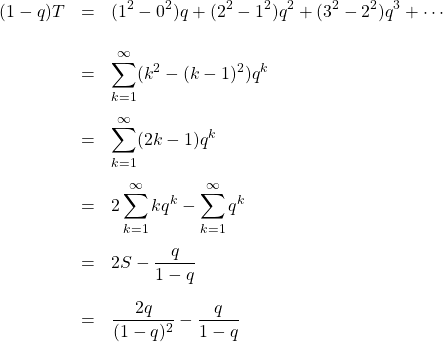
よって
![]()
となる。(教科書によっては
