>> 序,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18
ポアソン分布(2)どんな場面で使うか
ポアソン分布がモデル化するのは「互いに独立な無数のリスクのうち、一定時間内に顕在化する数」です。「無数に」という所がポイントで、例えば「明日一日の間に東京都内で起こる交通事故の件数」や「蚊がうようよしているやぶの中を5分間歩いたときに何回蚊に刺されるか」がこれに当たります。
1000匹の蚊が飛んでいるやぶを通り抜けることを考えましょう。一匹一匹があなたを刺す確率はそれぞれ0.002(0.2%)だとします。特定の蚊に刺される確率は微小ですが、何しろ1000匹もいるので、全く刺されずに済むのは難しそうです。あなたは何匹の蚊に刺されるでしょうか。
この状況は、すでに勉強した二項分布でモデル化できます。一匹一匹の蚊が刺すかどうかがベルヌーイ試行であると仮定すれば、蚊に刺される数は「![]() (飛んでいる蚊の数),
(飛んでいる蚊の数), ![]() (特定の蚊に刺される確率)の二項分布」です。期待値は
(特定の蚊に刺される確率)の二項分布」です。期待値は ![]() 匹ですから、平均的には2匹の蚊に刺されることになります。
匹ですから、平均的には2匹の蚊に刺されることになります。
このように二項分布でモデル化できるのですが、代わりにポアソン分布も使える、というのが今日の要点です。二項分布の代わりにポアソン分布を用いる場合、ポアソン分布のパラメータ ![]() の値は、
の値は、![]() に設定します。以下では、
に設定します。以下では、![]() ,
,![]() の二項分布と、
の二項分布と、![]() のポアソン分布で、0, 1, 2, 3,… が実現する確率を比較してみましょう。
のポアソン分布で、0, 1, 2, 3,… が実現する確率を比較してみましょう。
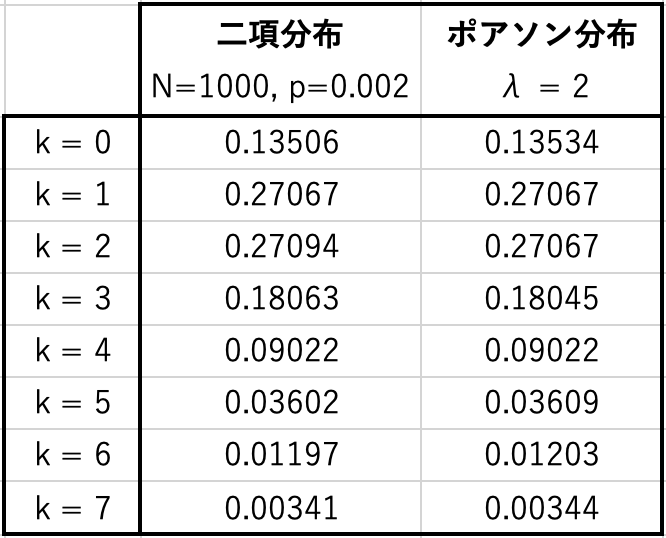
二項分布とポアソン分布とで、確率がほとんど同じであることが分かるでしょう。ほとんど同じになるのは、この例のように ![]() がとても大きくて、逆に
がとても大きくて、逆に ![]() はとても小さい状況です。そのような状況では、どちらの確率分布を用いても、確率はあまり変わりません。それでも、どちらかと言えばポアソン分布の方が好まれます。パラメータが1つで済みますし、蚊が何匹いるのかが曖昧でも済むからです。
はとても小さい状況です。そのような状況では、どちらの確率分布を用いても、確率はあまり変わりません。それでも、どちらかと言えばポアソン分布の方が好まれます。パラメータが1つで済みますし、蚊が何匹いるのかが曖昧でも済むからです。
二項分布で ![]() をどんどん大きくすると同時に、
をどんどん大きくすると同時に、![]() をどんどん小さくすると、ポアソン分布に近づいていくことは、数学的にも示せます。
をどんどん小さくすると、ポアソン分布に近づいていくことは、数学的にも示せます。
二項分布で ![]() が実現する確率は
が実現する確率は ![]()
ポアソン分布で ![]() が実現する確率は
が実現する確率は ![]()
でした。前者において、![]() が一定値
が一定値 ![]() になるように保ったまま、
になるように保ったまま、![]() を大きく(したがって
を大きく(したがって ![]() は小さく)して行くと後者に近づいていくことが示せるのです。証明を補論に示しますので、ぜひ挑戦してください。
は小さく)して行くと後者に近づいていくことが示せるのです。証明を補論に示しますので、ぜひ挑戦してください。
まとめ![]() が大きく、
が大きく、![]() が小さい二項分布は、ほぼポアソン分布であり、代わりにポアソン分布を使う方が好まれる。
が小さい二項分布は、ほぼポアソン分布であり、代わりにポアソン分布を使う方が好まれる。
次回はポアソン分布の期待値を計算します。
>> 確率分布(離散型)(15)ポアソン分布(3)期待値と分散
補論:二項分布がポアソン分布に収束することの証明
二項分布で ![]() が実現する確率を見てみましょう。まず、組み合わせの記号を階乗で表すと
が実現する確率を見てみましょう。まず、組み合わせの記号を階乗で表すと ![]() です。また、
です。また、 ![]() を用いれば
を用いれば ![]() は消去できます。すると
は消去できます。すると
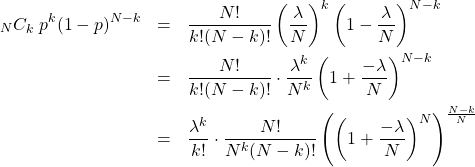
ここで
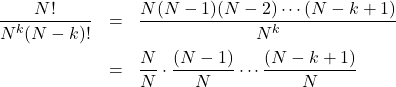
で、これは
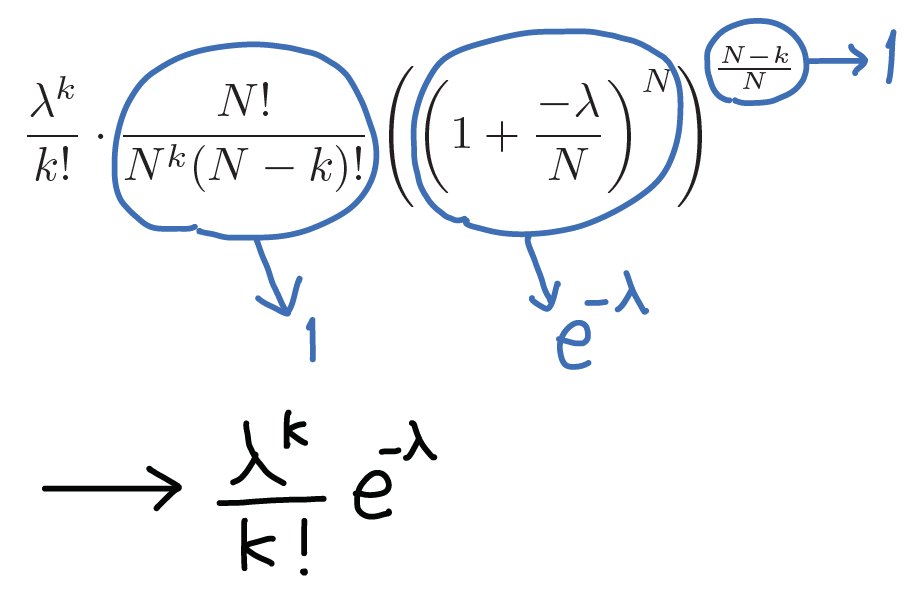
となり、ポアソン分布で ![]() が実現する確率に近づくことが示ました。
が実現する確率に近づくことが示ました。![]() に関してはオイラー数に関する項を復習してください。
に関してはオイラー数に関する項を復習してください。
