確率分布（離散型）（２） | 午後はカフェで経済学

>> 序，１，２，３，４，５，６，７，８，９，10，11，12，13，14，15，16，17，18

ベルヌーイ分布の期待値，分散，標準偏差

今日のテーマは、パラメータ $p$ のベルヌーイ分布の、期待値、分散、標準偏差を求めることです。以下の結果を導きます。

期待値（＝平均） $p$
分散　　　　 $p(1-p)$
標準偏差　 $\sqrt{p(1-p)}$

ベルヌーイ分布にしたがう確率変数を $X$ とおき、以下の表を使って、まず $X$ の期待値、次いで $X$ の分散と標準偏差を求めましょう。

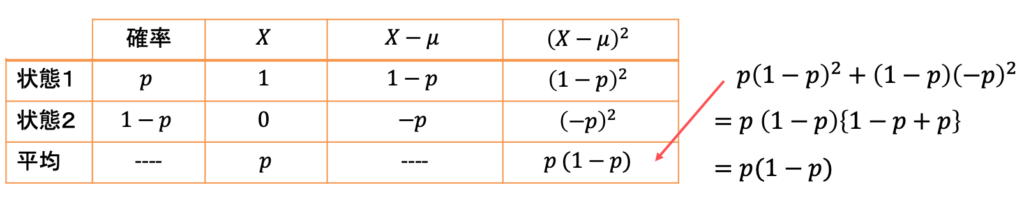
表の１列目、２列目は、「確率 $p$ で1，確率 $1-p$ で0」というベルヌーイ分布の定義を要約しています。期待値（＝平均）は、対応する実現値と確率を掛けてから合計したものなので、

$\begin{eqnarray*}p1+(1-p)0 = p\end{eqnarray*}$

となります。「確率 $0.2$ で1万円、確率0.8で0万円」というゲームの賞金ならば期待値は0.2万円ということです。

分散を求める手順は、表の３，４列目です。表の３列目では、実現値1と0が、平均 $p$ からどれだけ離れているかを計算しています（それぞれ $1-p$ ， $0-p$ です）。表の４列目で、それらを２乗しています。それを確率を使って足し合わせたものが分散ですから

$\begin{eqnarray*}p(1-p)^2+(1-p)(-p)^2 \end{eqnarray*}$

これを整理すると $p(1-p)$ となります。よって、ベルヌーイ分布の分散は $p(1-p)$ ，標準偏差はルートして $\sqrt{p(1-p)}$ となります。

次回はベルヌーイ分布以外の「二者択一」の分布を考えたいと思います。

>> 確率分布（離散型）（３）ベルヌーイ分布以外の「二者択一」分布