確率統計の入り口（４） | 午後はカフェで経済学

「過去のデータの標準偏差」と「確率変数の標準偏差」

前回、平均には２種類あることを説明しました。全部たして標本数Nで割る「過去のデータの平均」と、確率を使って求める「確率変数の平均」の２つです。

同じように、標準偏差にも、「過去のデータの標準偏差」と、「確率変数の標準偏差」の２つがあります。過去のデータの標準偏差は「格差の指標」です。テストの点数に関するクラスの標準偏差であれば、クラス内にどれくらい点数のばらつきがあるかを教えてくれます。標準偏差が大きいということは、平均よりずっと点数が高い人も、ずっと低い人もたくさんいたということです。

一方の確率変数の標準偏差は、将来起こりうることのばらつきですから、格差というより「リスクの指標」です。明日の最高気温の標準偏差が大きいということは、予報よりもうんと高い値が出る可能性もあるし、うんと低い値が出る可能性も結構あり、とても不確実であることを意味します。

ただ、そういう意味を知ることも大事ですが、きちんと計算できることの方がもっと大事です。そこで、確率変数の標準偏差の計算法を学ぶために、前回のルーレットの例で、賞金額の標準偏差を求めてみましょう。計算には確率の情報を用います。確率分布は以下の通りです。

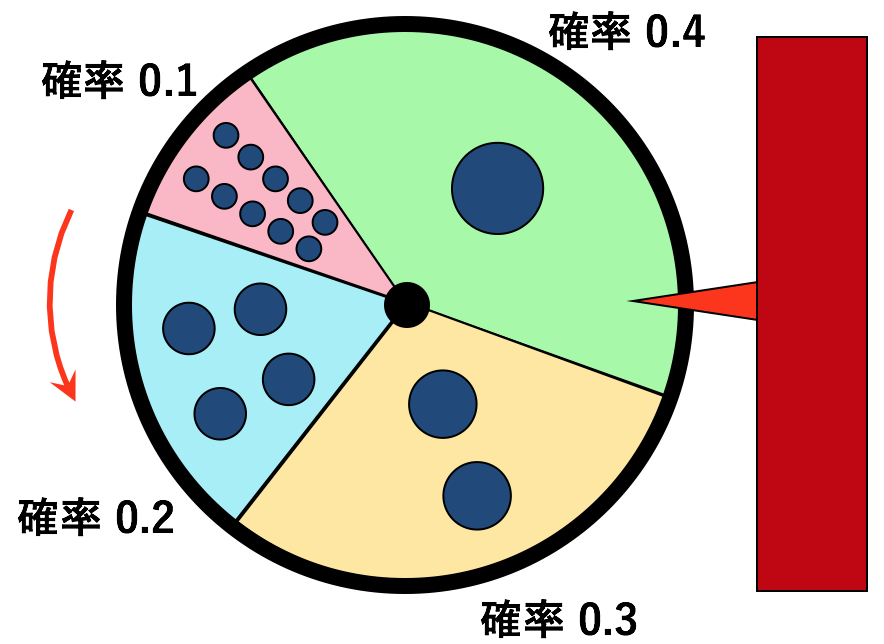
10万円（確率 0.1）
4万円（確率0.2）
2万円（確率0.3）
1万円（確率0.4）

標準偏差を計算する手順は、

手順１：平均を計算する
手順２：個々の値の「平均からのギャップ」を求める
手順３：「平均からのギャップ」をそれぞれ２乗した値の、平均を計算する
手順４：最後に平方根（ルート）を取る

となります。以前出てきた「過去のデータの標準偏差」の計算の手順と全く同じです。違うのは、手順１と３で平均を計算するときに確率を使うことだけです。手順１は10万、4万、2万、1万を、確率を使って平均します。前回もやりましたが、 $0.1(10)+ 0.2(4) + 0.3(2) + 0.4(1) = 2.8$ 万円でしたね。手順２で求めるのは、それぞれの値の「平均(2.8万円)からのギャップ」で、順番に $+7.2$ 万、 $+1.2$ 万、 $-0.8$ 万、 $-1.8$ 万です。手順３は、これの２乗、すなわち $(7.2)^2$ , $(1.2)^2$ , $(-0.8)^2$ , $(-1.8)^2$ を、確率を使って平均します。つまり $0.1(7.2)^2+0.2(1.2)^2+0.3(-0.8)^2+0.4(-1.8)^2=6.96$ です。手順４はこれの平方根をとるだけですから、標準偏差は $\sqrt{6.96}=2.64$ 万円となります。結果にばらつきのあるルーレットゲームであるほど、この値が大きくなるのです。

ちなみにですが、手順３までやって、手順４をやる前の中途の数字を「分散（ぶんさん）」と呼ぶので、後々のために名前を覚えてください。「分散」の平方根を取ると、「標準偏差」の完成です。

次は「２つの確率変数の相関係数」を勉強します。

>> 確率統計の入り口（５）２つの確率変数のあいだの相関係数