>> 序,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18
幾何分布(1)
ここまで「ベルヌーイ分布」と「二項分布」を勉強しました。3つ目は「幾何(きか)分布 (geometric distribution)」です。
ガチャガチャを当たりが出るまで続けるとしましょう。一度でも当たりが出たらストップです。毎回「当たる確率は0.2,外れる確率は0.8」で変わらないと仮定します。外れが続いた後は当たりが出やすい、ということはありません。このとき、
・ちょうど0回外れる確率(=1回目で当たる確率)は ![]()
・ちょうど1回外れる確率(=2回目で当たる確率)は ![]()
・ちょうど2回外れる確率(=3回目で当たる確率)は ![]()
となります。外れが10回、100回と続く確率も、小さいですがゼロではありません。「幾何分布」は、「当たりが出るまでに何回外れるか」の確率を教えてくれます。(*注1)
一般的な設定で説明します。![]() と
と ![]() という2つの結果だけが起こる「ベルヌーイ試行」を考えてください。コイン投げやバスケのシュートなどです。
という2つの結果だけが起こる「ベルヌーイ試行」を考えてください。コイン投げやバスケのシュートなどです。![]() が起こるまで、試行を何度も繰り返すことを考えましょう。このとき、起こりうるシナリオは以下の図にまとめられます。左上からスタートし、
が起こるまで、試行を何度も繰り返すことを考えましょう。このとき、起こりうるシナリオは以下の図にまとめられます。左上からスタートし、![]() が起こっている間は水色の線を右下に進み続け、一度でも
が起こっている間は水色の線を右下に進み続け、一度でも ![]() が起こったら黄色い線を右に進んで終わりです。
が起こったら黄色い線を右に進んで終わりです。![]() が起こる回数を
が起こる回数を ![]() で表すことにしましょう。
で表すことにしましょう。

ここで、各試行では「確率 ![]() で
で ![]() ,確率
,確率 ![]() で
で ![]() 」とします。すると、各シナリオが起こる確率は以下の図のようになります。
」とします。すると、各シナリオが起こる確率は以下の図のようになります。
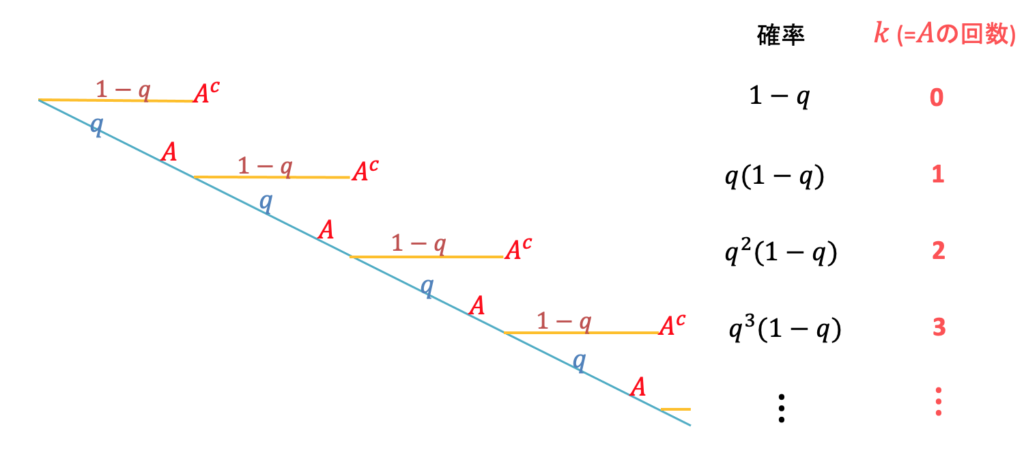
図の通り、1回も ![]() が起こらない確率は
が起こらない確率は ![]() ,ちょうど1回
,ちょうど1回 ![]() が起こる確率は
が起こる確率は ![]() ,ちょうど2回
,ちょうど2回 ![]() が起こる確率は
が起こる確率は ![]() ,・・・です。このように、幾何分布は「(
,・・・です。このように、幾何分布は「(![]() が起こるまでに起こる)
が起こるまでに起こる)![]() の回数」と確率の関係を表します。
の回数」と確率の関係を表します。
きちんと書き出せば、
確率 ![]() で0
で0
確率 ![]() で1
で1
確率 ![]() で2
で2
確率 ![]() で3
で3
![]()
確率 ![]() で
で ![]()
![]()
のようになります。これが幾何分布です。(*注2)
ところで、確率は全て足し合わせると1になります。次回はそれを確認したいと思います。
>> 確率分布(離散型)(10)幾何分布(2)確率の和が1であることの確認
*注1)
反対に、「外れが出るまでに何回当たるか」も幾何分布です。
*注2)
幾何分布の定義の仕方には、最後の1回も数に含めるバージョンもあります。その場合は全てに1を足して
確率 ![]() で1
で1
確率 ![]() で2
で2
確率 ![]() で3
で3
確率 ![]() で4
で4
・・・
となります。この場合、期待値は1増えます。
