>> 序，１，２，３，４，５，６，７，８，９，10，11，12，13，14，15，16，17，18
ベルヌーイ試行
次の確率分布を勉強する前に、知っておきたい言葉があります。「ベルヌーイ試行 (Bernoulli trial)」という言葉です。
ベルヌーイ試行の典型例は「コイン投げ」です。コインを投げたら、結果は表か裏かの２通りしかありません。また、複数回投げた場合、１回目の結果、２回目の結果、３回目の結果は‥‥全て互いに無関係ですね。このように、ベルヌーイ試行とは、
- ・１回の試行の結果は
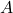または 
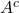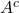（ は「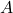 でない」の意味）の２通りしかない - ・ 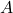が起こる確率は各試行共通であり、また各試行の結果は違いに独立（無関係）である
という２つの条件を満たす試行のことです。
１つめの条件の と の解釈は「成功と失敗」「合格と不合格」「当たりと外れ」など、何でも構いません。コイン投げでは表と裏が1/2ずつの確率で起こりますが、確率が半々である必要もありません。ただ、結果が２通りしかないので、 が起こる確率が 
であるならば、 が起こる確率は 
と決まります。
２つめの条件は、試行を繰り返すうちに確率が変わったりはしないことを要求しています。試験やスポーツの試合では、一度失敗すると自信を失ったり、逆に、失敗から教訓を得て失敗しにくくなったりします。そのような場合は、たとえ同じことを繰り返していても、「ベルヌーイ試行」とは言いません。コイン投げのように、毎回の結果が独立していて互いに影響しないことがベルヌーイ試行の条件です。
ベルヌーイ試行のイメージはできましたか。これを踏まえて、次回は「二項分布」を説明します。
今日のポイント
成功する確率と失敗する確率が、何度繰り返しても毎回 と で変わらない試行を「ベルヌーイ試行」という。