>> 序，１，２，３，４，５，６，７，８，９，10，11，12，13，14，15，16，17，18
ベルヌーイ分布
これから「離散型」の確率分布を５つ勉強します。トップバッターは「ベルヌーイ分布（Bernoulli distribution）」です。ベルヌーイ分布は0か1かの確率分布、すなわち
確率 
で1
確率 
で0
という確率分布です。例えば、当たりが出ると1万円もらえるくじを考えてください。ハズレの場合は何ももらえません。当たりは20%の割合で入っているとしましょう。するとこのくじの賞金は「確率0.2で1万円、確率0.8で0万円」ということですから、
のベルヌーイ分布です。
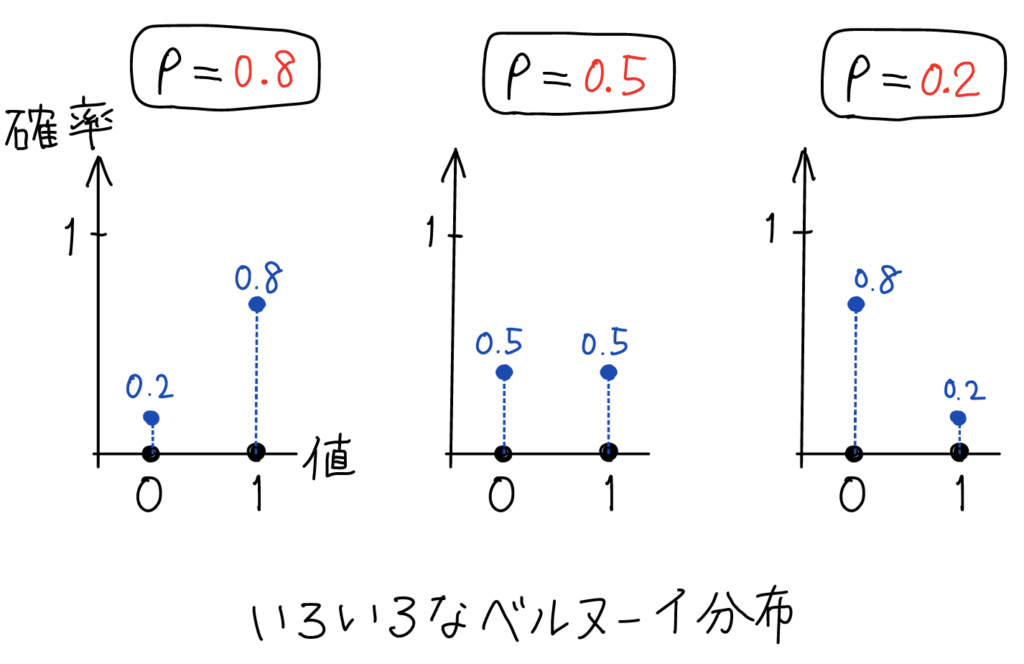
0または1の二者択一であるベルヌーイ分布は、確率分布の中で最も単純なものと言ってよいでしょう。成功か失敗か、受かるか落ちるか、女の子が生まれるか男の子が生まれるか等、結果が２つしかないときに、一方に0を、もう一方に1を割り当てればベルヌーイ分布になります。さまざまなベルヌーイ分布に関して、縦軸に確率を取ったグラフを描くと以下のようになります。
分布のパラメータ
０か１かという確率分布は全てベルヌーイ分布ですが、 が違えば異なるベルヌーイ分布です。 の値は、たくさんあるベルヌーイ分布を区別するためのいわば “IDナンバー”のような役割をしています。このような変数は「パラメータ」と呼ばれます。「放物線の式 
」の 
もパラメータです。 が異なれば、異なる放物線だからです。パラメータは、「◯◯分布」や「◯◯関数」など、同じグループに属する者どうしを区別してくれます。
次回はベルヌーイ分布の期待値、分散、標準偏差を計算します。
>> 確率分布（離散型）（２）ベルヌーイ分布の期待値・分散・標準偏差