>> 序,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18
イントロ
このシリーズでは「離散型の確率分布」を勉強します。まずはイントロダクションを兼ねて、いくつかの用語を説明します。
サイコロを振ったときに出る目の数は、
確率1/6で1
確率1/6で2
確率1/6で3
確率1/6で4
確率1/6で5
確率1/6で6
です。このように、どの値がどれくらいの確率で起こるのかを全て列挙したものを「確率分布(probability distribution)」と言います。起こりうる値のことは「実現値 (realized value)」と言います。サイコロには6通りの実現値があります。
確率分布はグラフでも表せます。横軸に実現値、縦軸に確率を取れば、サイコロの目の確率分布は以下のようになります。
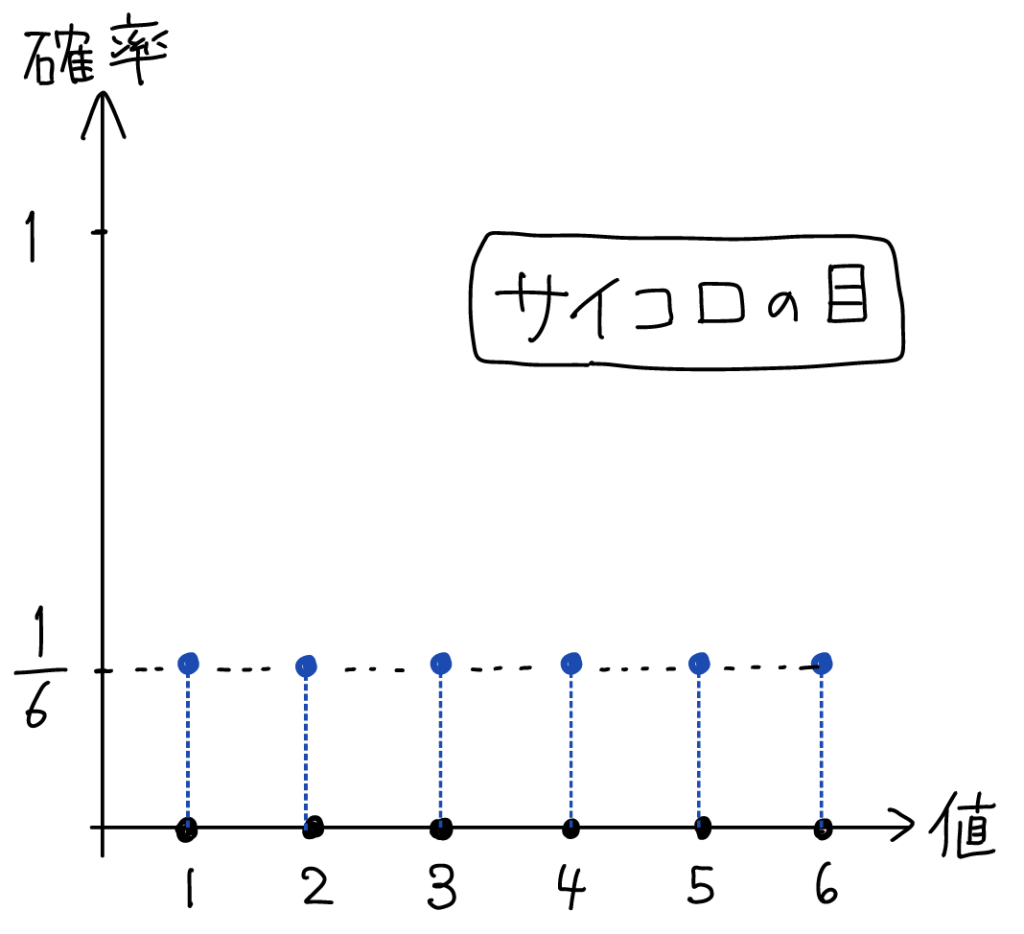
分布にはいろいろな名前が付いています。サイコロの目のように、全ての値が等確率で起こる確率分布は、「一様分布(uniform distribution)」と呼ばれます。「今日たまたま出会った人が何月生まれか」ということも、1から12が等確率で起こる一様分布と考えてよいでしょう。
次は、「サイコロ2個の目の合計」の確率分布を考えてみましょう。この場合は2から12の値が実現します。ただ、等確率ではありません。一番出にくいのは2と12、逆に一番出やすいのは7です。グラフにすると以下のようになります。
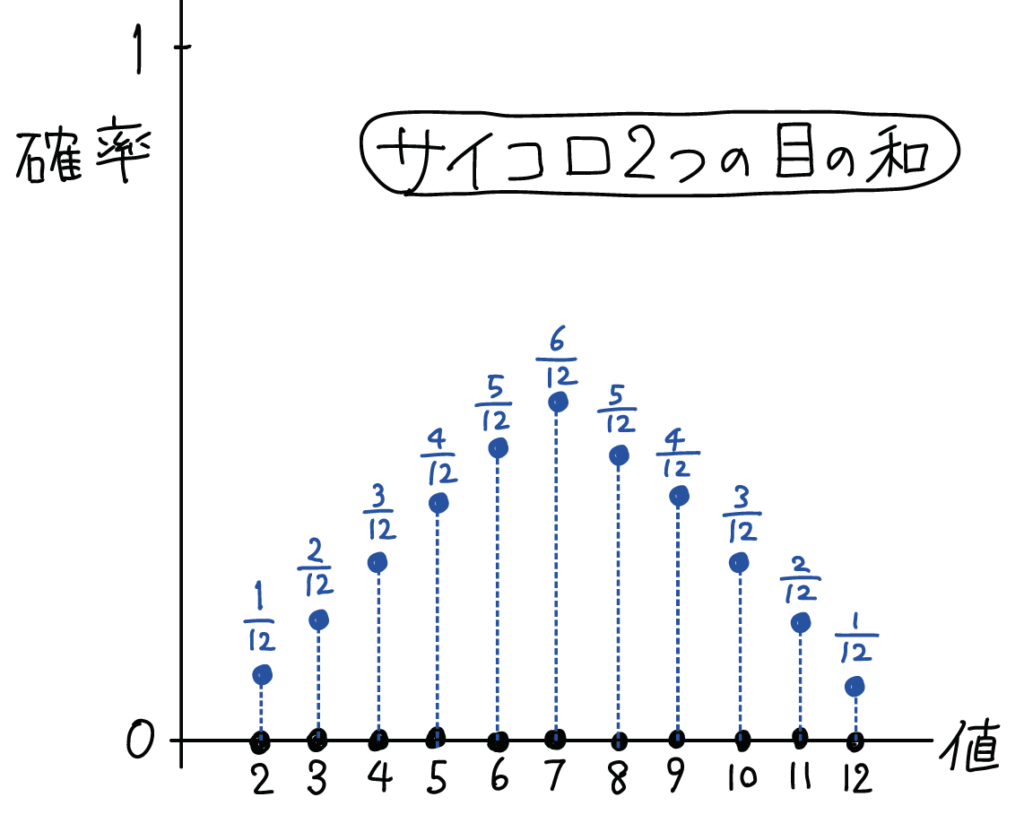
さて、確率分布には「離散型」と「連続型」の2種類があります。サイコロの目のように、飛び飛びの値しか取らない確率分布は「離散型 (discrete)」と呼ばれています。一方、気温や降水量や価格のように、理論上1.5でも1.55でも、どんな細かい値でも取り得る確率分布は「連続型 (continuous)」と呼ばれています。このシリーズの目的は、「離散型」の有名な確率分布を5つ勉強することです。5つとも日常生活のさまざまな場面で顔を出します。そのときに、「あ、これは◯◯分布だ!」と気付けるようになりましょう。
それでは始めます。初回は「ベルヌーイ分布(Bernoulli distribution)」です。
今日のポイント
・すべての実現値と確率を列挙したものを「確率分布」という。
・飛び飛びの値を取る確率分布は「離散型」である。
