>> 序,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18
二項分布 例2
前回は「二項分布」の例として ![]() の例を見ました。今日は
の例を見ました。今日は ![]() の例を見てみましょう。
の例を見てみましょう。
子供たちに人気のお菓子「ビックリマンチョコ」を1個買うと、確率 ![]() で「天使シール」が、確率
で「天使シール」が、確率 ![]() で悪魔シールが入っています。子供たちのお目当ては天使シールです。このお菓子を3個買ったときに、手に入る天使シールの枚数を
で悪魔シールが入っています。子供たちのお目当ては天使シールです。このお菓子を3個買ったときに、手に入る天使シールの枚数を![]() とおきましょう。
とおきましょう。![]() の実現値は、0,1,2,3のいずれかですが、それぞれの確率はいくつでしょうか。
の実現値は、0,1,2,3のいずれかですが、それぞれの確率はいくつでしょうか。![]() (3個とも天使シール)の確率は
(3個とも天使シール)の確率は ![]() です。
です。![]() (3個とも悪魔シール)の確率は
(3個とも悪魔シール)の確率は ![]() です。ここまでは簡単ですね。では
です。ここまでは簡単ですね。では ![]() (2個が天使シール)の確率はいくつでしょうか。
(2個が天使シール)の確率はいくつでしょうか。![]() のシナリオは3つあります。(悪魔,天使,天使)(天使,悪魔,天使)(天使,天使,悪魔)の3つです。1個目だけが悪魔シールである確率は
のシナリオは3つあります。(悪魔,天使,天使)(天使,悪魔,天使)(天使,天使,悪魔)の3つです。1個目だけが悪魔シールである確率は![]() です。2個目だけが悪魔シールである確率は
です。2個目だけが悪魔シールである確率は ![]() ,3個目だけが悪魔シールである確率は
,3個目だけが悪魔シールである確率は ![]() 。計算するとどのシナリオの確率も同じ
。計算するとどのシナリオの確率も同じ ![]() です。よって求める確率は
です。よって求める確率は ![]() となります。
となります。
あとで応用がきくよう、この考え方を図で表して理解を深めましょう。(図では「天使シール」を「成功」と呼んでいます。)
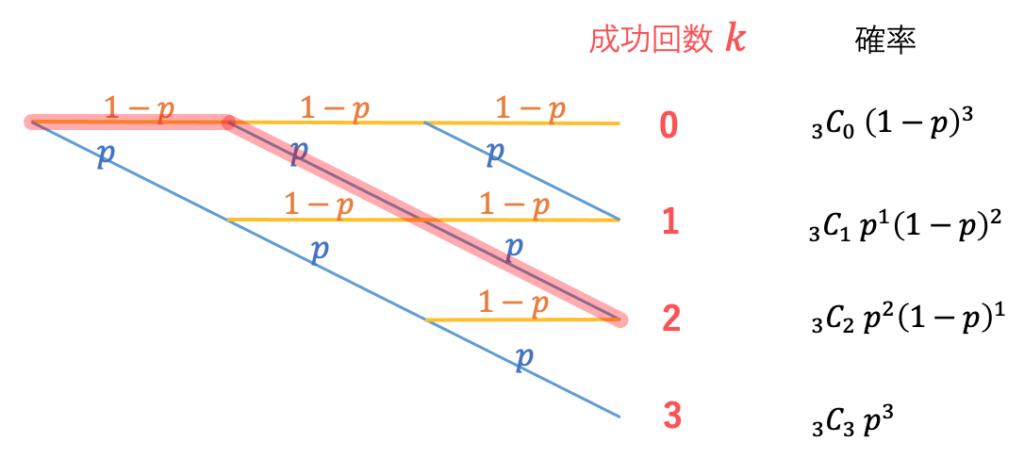
左上から出発し、試行の度に、成功したら下へ、失敗したらまっすぐ右へ進むとします。たとえば、赤線でなぞられているのは(失敗、成功、成功)というシナリオです。2回成功する確率を求めるためには、「2回成功するシナリオが何通りあるか」と「各シナリオの確率はいくつか」を考えます。2回成功するシナリオは ![]() 通りあり、1つ1つの確率は
通りあり、1つ1つの確率は ![]() なので、両者の積
なので、両者の積 ![]() が求める確率というわけです。
が求める確率というわけです。
一般に ![]() 回のうち
回のうち ![]() 回成功するというシナリオは
回成功するというシナリオは ![]() (
(![]() 個から
個から ![]() 個選ぶ組合せ)通りあり、各シナリオの確率は
個選ぶ組合せ)通りあり、各シナリオの確率は ![]() です(なぜなら
です(なぜなら ![]() 回成功、
回成功、![]() 回失敗だから)。よって、ちょうど
回失敗だから)。よって、ちょうど ![]() 回成功する確率は
回成功する確率は ![]() となります。
となります。
エクセルで確率を計算
二項分布に関する確率は、エクセルのBINOM.DIST関数を使って簡単に求めることができます。
この関数の引き数は4つで、順に「成功回数 ![]() 」「試行回数(size)
」「試行回数(size) ![]() 」「成功確率(prob)
」「成功確率(prob) ![]() 」「累積確率か否か(後述)」です。例えばコインを3回投げるときに、裏がちょうど0回、1回、2回出る確率はそれぞれ
」「累積確率か否か(後述)」です。例えばコインを3回投げるときに、裏がちょうど0回、1回、2回出る確率はそれぞれ
= BINOM.DIST(0, size=3, prob=0.5, FALSE)
= BINOM.DIST(1, size=3, prob=0.5, FALSE)
= BINOM.DIST(2, size=3, prob=0.5, FALSE)
です。
成功回数が「ちょうど◯回である確率」ならば最後の引き数はFALSEにしますが、「◯回以下である確率」の場合はTRUEにします。これは「累積確率」と呼ばれています。たとえば、コインを3回投げたときに裏が「2回以下」(つまり0回または1回または2回)である確率は
= BINOM.DIST(2, size=3, prob=0.5, TRUE)
です。エクセルでこの関数を実際に使ってみながら、5枚も10枚もコインを投げた場合の確率分布を求めてみてください。
次回は、二項分布の期待値と分散がどうなるかを説明します。
今日のポイント
パラメータが ![]() の二項分布で実現値が
の二項分布で実現値が ![]() となる確率は、
となる確率は、![]() である。
である。
>> 確率分布(離散型)(7)二項分布の期待値,分散,標準偏差

