目次

<< １，２，３，４，５，６，７，８，９，10，11，12，13，14，15，16，17

行列のかけ算１　Ax


今回から、行列のかけ算を勉強します。行列のかけ算は、概念的には難しくないのですが、ルールを覚えなくてはいけません。初回の今日は、「行列と縦ベクトルのかけ算」です。「ベクトルの内積」を知っていると理解が速いので、そちらも復習してください。


１つめの例は、A が3行2列の行列、x が成分２つの縦ベクトルの場合です。すなわち

    \begin{eqnarray*} A= \left( \begin{array}{cc} a_{1,1}& a_{1,2}\\ a_{2,1} & a_{2,2}\\ a_{3,1} & a_{3,2} \end{array} \right), \hspace{10mm} x=\left( \begin{array}{c} x_{1}\\ x_{2} \end{array} \right) \end{eqnarray*}


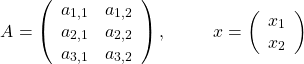
このとき、２つの積は以下のように書きます。

    \begin{eqnarray*} Ax= \left( \begin{array}{cc} a_{1,1}& a_{1,2}\\ a_{2,1} & a_{2,2}\\ a_{3,1} & a_{3,2} \end{array} \right) \left( \begin{array}{c} x_{1}\\x_{2} \end{array} \right) \end{eqnarray*}


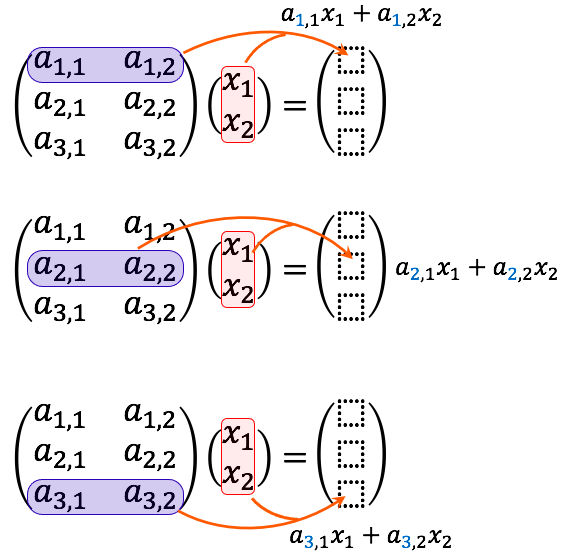
これの定義、すなわち、計算のしかたを説明しましょう。以下の図のように、Aの各行と x の内積を求め、結果を縦に並べます。たとえば、行列Aの１行目と x との内積は a_{1,1} \; x_1 + a_{1,2} \; x_2 ですね。同様に、A の２行目や３行目に関しても、x との内積を求めます。


例題をやってみましょう。次のかけ算を計算してください。

    \begin{eqnarray*} \left( \begin{array}{cc} 1&2\\ 3 & 4\\ 5 & 6 \end{array} \right) \left( \begin{array}{c} 10\\30 \end{array} \right) \end{eqnarray*}


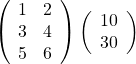
手順を図であらわすと


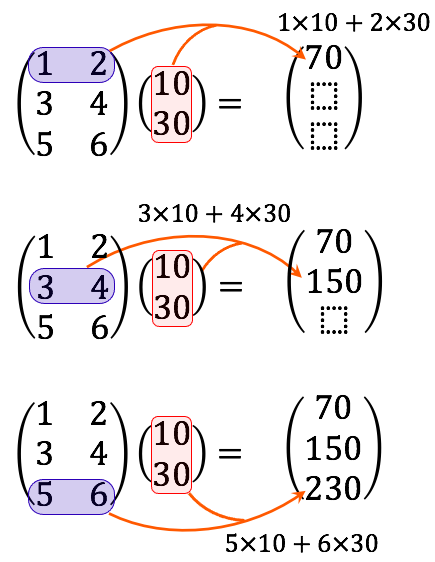
ですから、正解は 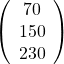\left( \begin{array}{c} 70\\150 \\230 \end{array} \right) となります。どうしてこのような定義になったのかは、そのうち機会があれば勉強しましょう。今はとにかく定義を頭に入れてください。


２つめの例は、2行3列の行列 B と、成分が３つの縦ベクトル y のかけ算です。

    \begin{eqnarray*} By= \left( \begin{array}{ccc} b_{1,1}& b_{1,2} & b_{1,3}\\ b_{2,1} & b_{2,2} & b_{2,3} \end{array} \right) \left( \begin{array}{c} y_{1} \\ y_{2} \\ y_3 \end{array} \right) \end{eqnarray*}


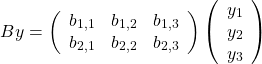
これも同じです。行列 B の各行と y との内積を求めて縦に並べます。


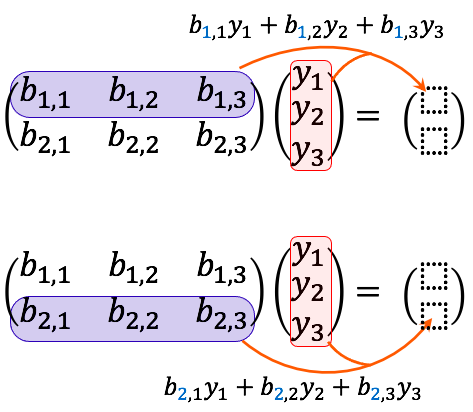
実際の数値例も挙げておくので、ぜひ自分で確かめてみてください。

    \begin{eqnarray*} \left( \begin{array}{ccc} 5& 10 & 15\\ 0.5 & 1 & 2 \end{array} \right) \left( \begin{array}{c} 4\\ 0 \\ 8 \end{array} \right) = \left( \begin{array}{c} 140 \\ 18 \end{array} \right) \end{eqnarray*}


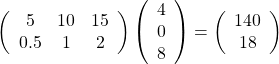
ここで注目してほしい点が２つあります。１つめは、行列の横のサイズ（すなわち列の数）と、ベクトルのサイズが一致していないと、この計算はできないという点です。もうひとつは、計算結果のサイズがどうなるか、という点です。計算結果のサイズは A に何行あるかで決まります。


いくつか例題を挙げておきますので、練習して慣れてください。


例題１（解答はこちら）

    \begin{eqnarray*} \left( \begin{array}{cc} 1& 2\\ 3 & 4\\ 5 & 6 \\ 7&8 \end{array} \right) \left( \begin{array}{c} 5\\10 \end{array} \right) \end{eqnarray*}


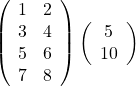
例題２（解答はこちら）

    \begin{eqnarray*} \left( \begin{array}{cccc} 0.1 & 0.2& 0.3 & 0.4 \end{array} \right) \left( \begin{array}{c} 1\\5 \\10 \\15 \end{array} \right) \end{eqnarray*}




Excel で計算する場合




エクセルで計算する場合は、計算結果のベクトルのサイズをあらかじめ予想したうえで、結果を表示したい領域を選択します。



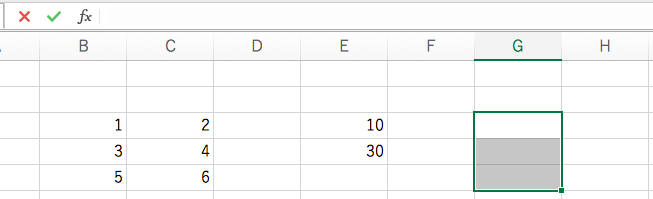
そのうえで、上部の数式バーから、数式を入力します。数式は＝で始め、関数名を入力します。使用する関数は MMULT という名前です。行列が英語で Matrix，かけ算が英語で Multiplication なので、このような名前がついています。関数に、かけ合わせたい行列と縦ベクトルの位置を、コンマで区切って順番に与えます。すると、選んだ範囲が自動的にカラーでハイライトされます。



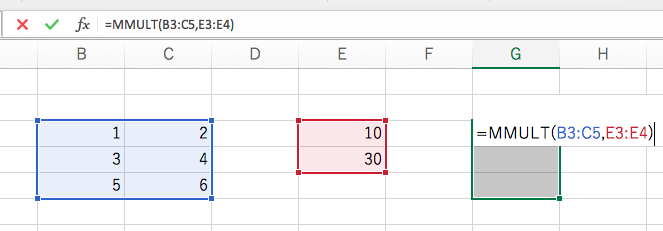
最後に、「確定」するときは Ctrl + Shift + Enter を同時に押します。Enterキーだけを押してもうまくいきません。エクセルでは行列がらみの関数を使う際は、確定するときに Ctrl + Shift + Enter を押さなければならないという決まりがあるからです。（計算の一部を修正するだけの場合もです。）




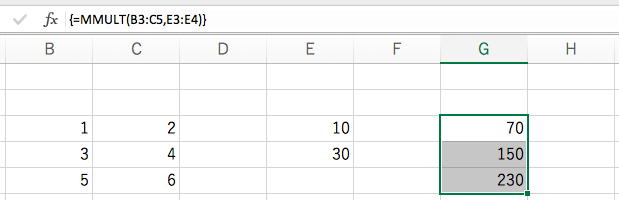
「行列と縦ベクトル」の積はできるようになりましたか。次回は「横ベクトルと行列」の積です。

>> 行列の基本（５）行列のかけ算２　xB


今回のまとめ

  1. 行列と縦ベクトルのかけ算では、行列を行に分け、それぞれ縦ベクトルと内積を取る。
  2. 行列の列の数とベクトルのサイズが一致している必要あり。
  3. エクセルで計算する場合はMMULT関数を用いる。

例題１の解答（戻る）

    \begin{eqnarray*}&&\left( \begin{array}{cc} 1& 2\\ 3 & 4\\ 5 & 6 \\ 7&8 \end{array} \right) \left( \begin{array}{c} 5\\10 \end{array} \right)\\\\ &=&\left( \begin{array}{c} 1\times 5 + 2\times 10\\ 3\times 5 + 4\times 10 \\ 5\times 5 + 6\times 10 \\ 7\times 5 + 8\times 10 \end{array} \right)\\\\&=& \left( \begin{array}{c} 25\\ 55 \\ 85\\ 115 \end{array} \right) \end{eqnarray*}

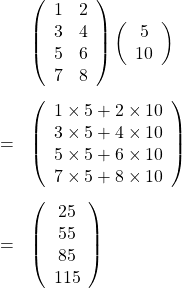
例題２の解答（戻る）

    \begin{eqnarray*} && \left( \begin{array}{cccc} 0.1 & 0.2& 0.3 & 0.4 \end{array} \right) \left( \begin{array}{c} 1\\5 \\10 \\15 \end{array} \right)\\\\ &=& 0.1\times 1 + 0.2 \times 5 + 0.3 \times 10 + 0.4 \times 15 \\\\&=& 10.1 \end{eqnarray*}


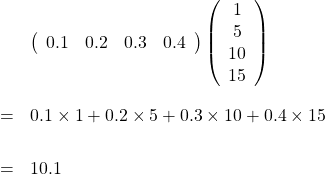
　答えに数字が１つしかないのは、先行する行列に１行しかないからです。