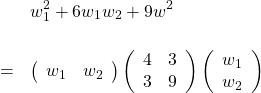行列の基本（１７） | 午後はカフェで経済学

<< １，２，３，４，５，６，７，８，９，10，11，12，13，14，15，16，17

理解度チェック正誤問題

ここまで勉強したことの理解度チェックです。紙とペンの用意をお願いします。以下の各文の内容が、正しいか誤りかを答えてください。

問１（解説）
$3 \times 4$ の行列には、列が３列ある。

問２（解説）
１列に含まれる成分の数は、その行列の行の数に等しい。

問３（解説）
$A$ が $3 \times 3$ の行列、 $B$ が $3 \times 4$ の行列であるとき、積 $AB$ を計算することはできない。

問４（解説）
$A$ も $B$ も $3 \times 4$ の行列であるとき、積 $AB$ を計算することはできない。

問５（解説）
$m$ 行 $n$ 列の行列と、 $n$ 行 $k$ 列の行列を掛けると、結果は $m$ 行 $k$ 列となる。

問６（解説）
$AB$ と $BA$ は等しいとはかぎらない。

問７（解説）
$(AB)C$ と $A(BC)$ は等しいとはかぎらない。

問８（解説）
転置行列が存在するのは、正方行列だけである。

問９（解説）
ある行列を転置すると、行の数と列の数が逆転する。

問10（解説）

$\left( \begin{array}{ccc} 1& 3 & 5\\ 2 & 4 & 6 \end{array} \right)$ には逆行列は存在しない。

問11（解説）
逆行列が存在しない正方行列もある。

問12（解説）
単位行列の転置行列は単位行列である。

問13（解説）
単位行列の逆行列は単位行列である。

問14（解説）

$\left(\begin{array}{cc} 1& 1 \\ 1& 2 \end{array} \right)$ の逆行列は

$\left( \begin{array}{cc}2& -1 \\-1& 1\end{array} \right)$ である。

問15（解説）

$4w_1^2 + 6w_1w_2 + 9w_2^2$ を行列の積で表すと、真ん中にくる行列は

$\begin{eqnarray*}\left( \begin{array}{cc} 4& 3 \\ 3 & 9 \end{array} \right)\end{eqnarray*}$

である。

どうだったでしょうか。正解は

です。全問できていればひとまず合格です。ごくろうさまでした。

解答（順不同）

問１（戻る）
正解は「誤」です。 $3\times 4$ の行列には列が４列あります。
（第１回　名称）

問５（戻る）
正解は「正」です。
（第７回　行列のかけ算４　サイズ）

問９（戻る）
正解は「正」です。
（第９回　行列の転置）

問13（戻る）
正解は「正」です。単位行列と単位行列をかけたら単位行列になるので、逆行列の定義を満たします。

問２（戻る）
正解は「正」です。
（第１回　名称）

問６（戻る）
正解は「正」です。行列の並び順を変えると、かけ算の結果は変わります。
（第６回　行列のかけ算３　AB）

問10（戻る）
正解は「正」です。逆行列があるのは、正方行列だけです。
（第11回　逆行列の定義）

問14（戻る）
正解は「正」です。２つを掛けると単位行列になることを確認しましょう。

問３（戻る）
正解は「誤」です。Aの列数とBの行数が一致しているので、積を計算することができます。
（第７回　行列のかけ算４　サイズ）

問７（戻る）
正解は「誤」です。行列の並び順が変わらなければ、どこから計算しても同じです。
（第８回　行列のかけ算５　ABC）

問11（戻る）
正解は「正」です。第13回でそのような例を紹介しました。

問15（戻る）
正解は「正」です。

$\begin{eqnarray*}&& w_1^2 + 6w_1w_2 + 9w^2 \\\\&=& \left( \begin{array}{cc}w_1 & w_2 \end{array} \right)\left( \begin{array}{cc} 4& 3 \\ 3 & 9 \end{array} \right)\left( \begin{array}{c} w_1 \\ w_2 \end{array} \right)\end{eqnarray*}$

となります。
（第16回　二次形式の行列表記）

問４（戻る）
正解は「正」です。Aの列数とBの行数が一致していないので、積を計算できません。
（第７回　行列のかけ算４　サイズ）

問８（戻る）
正解は「誤」です。転置は縦横をひっくり返すだけなので、正方行列でなくてもできます。
（第９回　行列の転置）

問12（戻る）
正解は「正」です。単位行列は、縦横をひっくり返しても変わりません。
（第10回　単位行列）