<< 1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17
行列の積で表す1 連立一次方程式
中学校の数学では、「式の展開」の反対の操作として、「因数分解」を教わりました。「行列の積の計算」の反対の操作は、「行列の積で表す」ことです。
例えば
![]()
という2つの式は
![]()
と表せます。ということは、
![]()
という連立方程式は
![]()
と書き表せます。これが、「行列の積で表す」ということです。
今度は、3変数
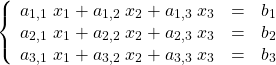
という連立方程式はどうでしょうか。これは
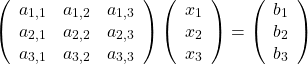
と書けるので
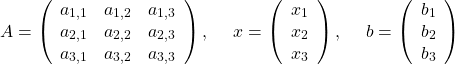
とおけば、
![]()
と書けます。
連立一次方程式をこのように表したあと、大学の先生は「両辺の左から逆行列をかけると‥‥
![]()
‥‥はい、これで連立方程式が解けました」と言います。「いやいや、ちょっと待ってください、解けてないでしょ。
次の連立一次方程式を、エクセルで解いてみましょう。
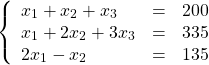
まず係数行列

そのうえで、![]() を計算します。
を計算します。![]() の逆行列には MINVERSE 関数を、これと
の逆行列には MINVERSE 関数を、これと ![]() との積には MMULT 関数を使います。
との積には MMULT 関数を使います。
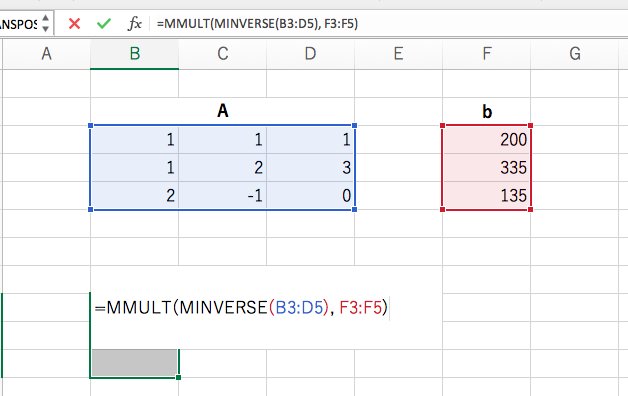
確定はいつもどおり、Ctrl + Shift + Enter です。
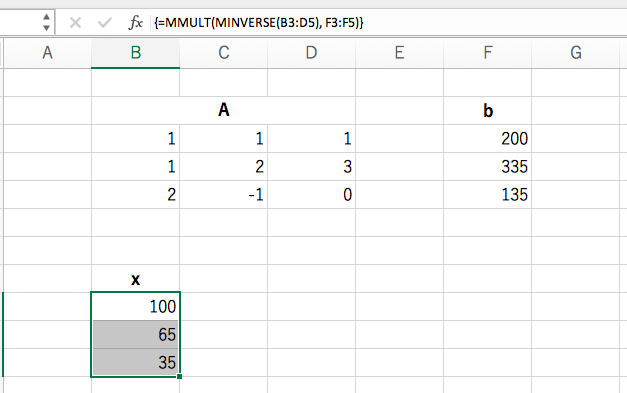
答えは ![]() です。この方法で、たとえ変数が100個あっても、連立一次方程式は一瞬にして解くことが可能です。
です。この方法で、たとえ変数が100個あっても、連立一次方程式は一瞬にして解くことが可能です。
今回は連立1次式を行列の積で表しました。次回は2次式を行列で表してみたいと思います。
>> 行列の基本(16)行列の積で表す2 二次形式
