目次

<< １，２，３，４，５，６，７，８，９，10，11，12，13，14，15，16，17

逆行列４　「両辺に逆行列を掛けると」


中学校の数学では、例えば ab = c のとき、「両辺を a で割って」b=c/a であるという変形のしかたを教わります。行列にも類似の式変形があるので、今回はそれを勉強しましょう。


今、A, B, C は全て行列だとして、

    \begin{eqnarray*} AB = C \end{eqnarray*}


という式を考えましょう。A は正方行列だとします。このとき、両辺に、左から逆行列 A^{-1} を掛けてみましょう。すると

    \begin{eqnarray*} A^{-1}AB = A^{-1}C \end{eqnarray*}


となります。わざわざ「左から」と断るのは、行列のかけ算にとってはかけ算の順番が大事だからです。


ここで、逆行列の定義を思い出すと、A^{-1}A の部分は「単位行列」に等しくなることがわかります。単位行列は、掛けても掛けなくても同じなので、結局 B = A^{-1}C となります。これは、Aの逆行列が存在する場合にのみできる変形です。


最初からまとめると、

    \begin{eqnarray*} AB &=& C\\A^{-1} AB &=& A^{-1}C\\B &=& A^{-1}C \end{eqnarray*}


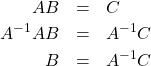
となります。この「両辺の左から（または右から）逆行列を掛けると・・・」というフレーズはよく出てくるので、慣れてくださいね。


さて、公式やエクセルを使って逆行列を瞬時に求められると、さまざまなメリットがあります。その１つが、連立一次方程式を瞬時に解けるようになることです。次回はそれを説明します。

>> 行列の基本（１５）行列の積で表す１　連立一次方程式