目次

<< １，２，３，４，５，６，７，８，９，10，11，12，13，14，15，16，17

逆行列２　2×2の逆行列の公式


前回、逆行列とは何かを説明しました。今回はその求め方です。サイズが 2\times2 の行列に関しては、逆行列を求めるための公式が存在します。公式は

    \begin{eqnarray*} \left( \begin{array}{cc} a& b \\ c& d \end{array} \right)^{-1} = \frac{1}{ad-bc}\left( \begin{array}{cc} d& -b \\ -c& a \end{array} \right). \end{eqnarray*}


係数の分母にある ad-bc は、数学でたびたび目にする表現ですから、いずれ覚えるでしょう。あとは行列の中の a と d の場所を入れ替え、b と c にマイナスをつけるだけで出来上がりです。


公式がうろ覚えで自信が持てないときは、実際に元の行列にかけて単位行列になることを確認してから使ってください。

    \begin{eqnarray*} && \frac{1}{ad-bc}\left( \begin{array}{cc} d& -b \\ -c& a \end{array} \right) \left( \begin{array}{cc} a& b \\ c& d \end{array} \right)\\ \\&=&\frac{1}{ad-bc}\left( \begin{array}{cc} ad-bc& -ab+ab \\ cd-cd& -cb+ad \end{array} \right)\\ \\&=& \left( \begin{array}{cc} 1& 0 \\ 0& 1 \end{array} \right) \end{eqnarray*}


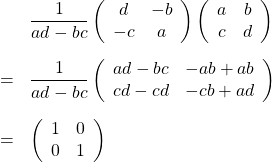
公式を使う数値練習です。

    \begin{eqnarray*} A = \left( \begin{array}{cc} 1& 2 \\ 3 & 4 \end{array} \right) \end{eqnarray*}


のとき、公式を使って逆行列を求めてみましょう。答えは、ad - bc = -2 より、

    \begin{eqnarray*} A^{-1} &=& \frac{1}{-2}\left( \begin{array}{cc} 4& -2 \\ -3 & 1 \end{array} \right) \\ \\&=& \left( \begin{array}{cc} -2& 1 \\ 1.5 & -0.5 \end{array} \right) \end{eqnarray*}


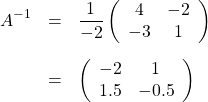
となります。


もっと大きな行列、例えば 3 \times 3 の行列だと、暗記できるような逆行列の公式はありません。そのような場合はエクセルを使って逆行列を求めましょう。次回は、エクセルで逆行列を計算する方法を説明します。

>> 行列の基本（１３）逆行列３　エクセルで逆行列