<< 1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17
行列の転置
行列の転置 (Transpose) とは、行列の縦横をひっくり返すことです。例えば
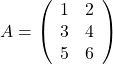
であるとき、
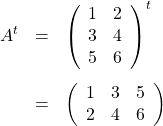
を意味します。
転置によって、横ベクトルは縦ベクトルに、縦ベクトルは横ベクトルになります。文章中では、
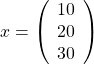 などと書くと行間が開き過ぎる原因となるので、転置記号の
などと書くと行間が開き過ぎる原因となるので、転置記号の エクセルで行列を転置するときに使うのは、TRANSPOSE 関数です。転置したい行列の範囲を指定します。
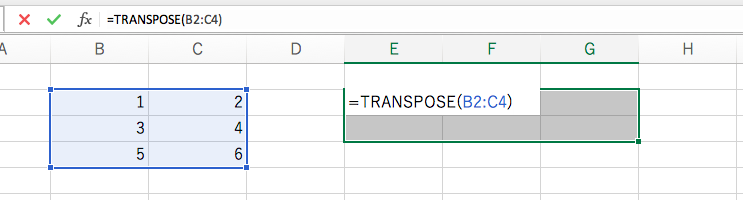
これも行列関数なので、確定のときは Ctrl + Shift + Enter を同時に押してください。
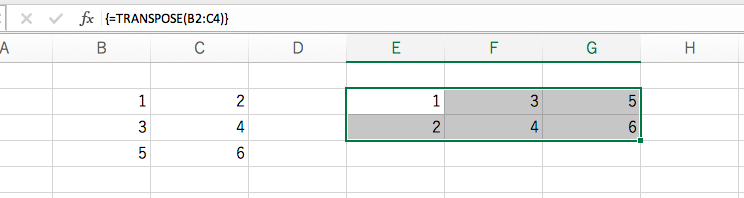
行列の転置は縦横を逆転するだけで、これ自体は大したことはありません。しかし、行列のかけ算との兼ね合いで、大事な定理が1つあります。それは
![]()
![]()
というふうに、行列の積を計算してから転置したものと、それぞれの行列を転置したものを逆順にかけ算したものが、同じになるという定理です。(証明へ)
具体例を1つ見てみましょう。
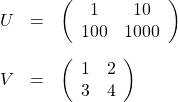
のとき、
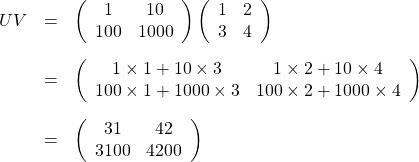
ですから、
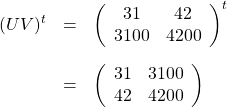
です。一方、
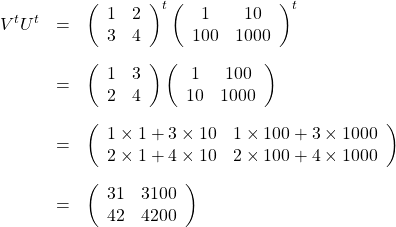
ですから、
次回は「単位行列」という特別な行列を紹介します。
>> 行列の基本(10)単位行列
定理の証明:(戻る)![]() を証明するには、
を証明するには、
「![]() の第
の第 ![]() 成分 =
成分 = ![]() の第
の第 ![]() 成分」
成分」
となることを証明する。![]() の 第
の 第 ![]() 成分
成分
= ![]() の 第
の 第 ![]() 成分
成分
= ![]() の第
の第 ![]() 行 と
行 と ![]() の第
の第 ![]() 列の内積
列の内積
である。一方、![]() の第
の第 ![]() 成分
成分
= ![]() の第
の第 ![]() 行と
行と ![]() の第
の第 ![]() 列の内積
列の内積
= ![]() の第
の第 ![]() 列と
列と ![]() の第
の第 ![]() 行の内積
行の内積
よって両者は等しいことを確かめられた。
2つの行列で成り立つならば、帰納的に3つ以上でも成立することが証明できる。すなわち、![]()
