<< 1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17
行列のかけ算3 AB
次は2つの行列のかけ算です。例として、次の2つの行列の積を考えましょう。
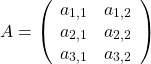
![]()
まず、積
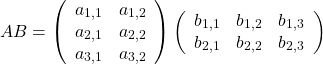
先行する

そして、![]() から1行、
から1行、![]() から1列取ってきて、内積を求めます。例えば、
から1列取ってきて、内積を求めます。例えば、![]() の1行目と
の1行目と ![]() の1列目の内積は、第
の1列目の内積は、第![]() 成分に書き込みます。
成分に書き込みます。

![]() が3行、
が3行、![]() が3列を有するので、
が3列を有するので、![]() 通りの組み合わせがあります。以下の数値例では、
通りの組み合わせがあります。以下の数値例では、![]() の各行、
の各行、![]() の各列を色分けして表示してあります。
の各列を色分けして表示してあります。

この例では、![]() が3行、
が3行、![]() が3列を有するので、
が3列を有するので、![]() のサイズは
のサイズは ![]() になりました。
になりました。
つぎに、積![]() を考えましょう。
を考えましょう。
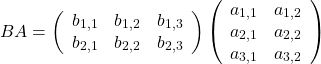
先行する

かけ算の結果はサイズが ![]() の行列となります。さっきと同じ数値例で
の行列となります。さっきと同じ数値例で ![]() を計算してみましょう。
を計算してみましょう。

![]() と
と ![]() は結果が異なっていますね。行列のかけ算は、順番が変われば別物なのです。
は結果が異なっていますね。行列のかけ算は、順番が変われば別物なのです。
エクセルによる計算は、動画に示しておきます。
「かけ算の順番をひっくり返すと答えが変わる」ことの確認も兼ねて、1つ例題をやってみましょう。
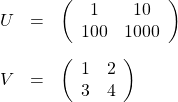

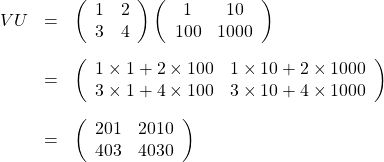
となります。
すでに気づいている人もいるかもしれませんが、行列のかけ算の結果が、どんなサイズの行列になるかは、もとの2つの行列のサイズによって決まります。次回はそれを整理したいと思います。
>> 行列の基本(7)行列のかけ算4 行列のサイズ
