目次

<< １，２，３，４，５，６，７，８，９，10，11，12，13，14，15，16，17

行列の和とスカラー倍


２つの行列の「和」は、成分ごとに足し算するだけです。例えば

    \begin{eqnarray*} A&=&\left( \begin{array}{cc} 1& -2 \\ 3 & 5.5 \end{array} \right)\\\\B&=&\left( \begin{array}{cc} 10& 100 \\ 10 & 1000 \end{array} \right) \end{eqnarray*}


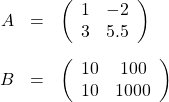
であれば、

    \begin{eqnarray*} A+B&=& \left( \begin{array}{cc} 1& -2 \\ 3 & 5.5 \end{array} \right) + \left( \begin{array}{cc} 10& 100 \\ 10 & 1000 \end{array} \right) \\ \\&=& \left( \begin{array}{cc} 1+10& -2+100 \\ 3+10 & 5.5+1000 \end{array} \right)\\ \\&=& \left( \begin{array}{cc} 11& 98 \\ 13 & 1005.5 \end{array} \right) \end{eqnarray*}


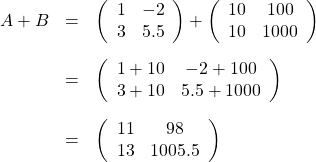
です。引き算も同じで、成分ごとに差を求めるだけです。成分ごとなので、行列AとBのサイズが一致していないと足し算や引き算はできないことが分かります。


次は「スカラー倍」です。１つの数字のことを「スカラー」と呼ぶと前回説明しましたが、行列のスカラー倍は、各成分にその数字を掛けることです。例えば

    \begin{eqnarray*} 10\times A &=& 10\times \left( \begin{array}{cc} 1& -2 \\ 3 & 5.5 \end{array} \right)\\ \\&=& \left( \begin{array}{cc} 10& -20 \\ 30 & 55 \end{array} \right) \end{eqnarray*}


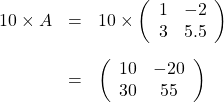
です。


次は行列の積（かけ算）です。行列のかけ算は複雑なので、これから何回かかけてじっくり勉強していきます。

>> 行列の基本（３）行列の「成分ごとのかけ算」