<< 1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17
行列の積で表す2 二次形式
今日のテーマは、「2次式」を行列を使って表すことです。2次式というと、例えば ![]() のような式を思い浮かべますが、今日扱うのは、1次の項や定数項を含まない、純粋な2次式です。そのような純粋な2次式を「二次形式 (quadratic form)」と言います。例えば
のような式を思い浮かべますが、今日扱うのは、1次の項や定数項を含まない、純粋な2次式です。そのような純粋な2次式を「二次形式 (quadratic form)」と言います。例えば
1変数 ![]() の二次形式:
の二次形式:
![]()
2変数
![]()
ここで、
二次形式は、行列で表すことができます。例えば
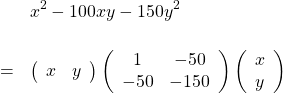
というふうに、3つの行列の積で表せるのです。
やり方は簡単です。2変数の場合、まずは
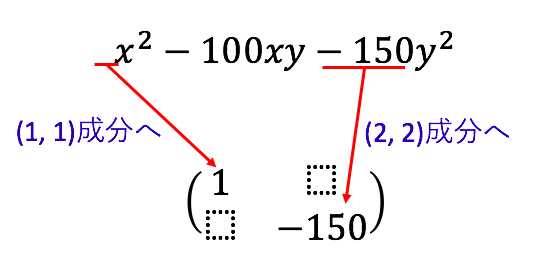
次に、![]() の係数
の係数 ![]() を、半分にして(1,2)成分と(2,1)成分の両方に書き込みます。
を、半分にして(1,2)成分と(2,1)成分の両方に書き込みます。

そうして出来上がった行列を、![]() と
と ![]() でサンドイッチして完了です。正式ではありませんが、この形で表した二次形式を、サンドイッチ型 (sandwich form)と呼ぶこともあります。
でサンドイッチして完了です。正式ではありませんが、この形で表した二次形式を、サンドイッチ型 (sandwich form)と呼ぶこともあります。
サンドイッチ型を展開して、元に戻ることを確認しておきましょう。展開すると
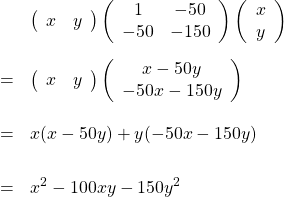
ですから、最初の二次形式に戻ります。
3変数の場合も同様です。3変数
![]()
です。2乗の項が3つ、交差項が3つありますね。これも、正方行列を

です。真ん中の行列では、2乗の項の係数 131, 58, 24 は対角成分に並べます。一方、交差項の係数は、2分の1して非対角成分に並べます。並べ方は (1,2)成分と(2,1)成分には
二次形式で表される関数は、このように行列表記しておくと、関数の値を求めたいときに、エクセルの MMULT 関数を使って素早く計算することができます。
さて、これで行列の基本の勉強は終わりです。次回はここまでの理解度チェックをしてみましょう。
>> 行列の基本(17)理解度チェック正誤問題
