<< 1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17
単位行列
行の数と列の数が等しい行列を「正方行列 (Square matrix)」と言います。正方形の形をしているからです。
正方行列の左上から右下へ至る対角線上の成分を「対角成分 (diagonal components)」と言います。それ以外は「非対角成分 (off-diagonal components)」です。図で表すと、赤い所が対角成分、青い所が非対角成分です。

対角成分が全て1、非対角成分が全て0である正方行列を「単位行列 (Unit matrix)」と言います。例えば
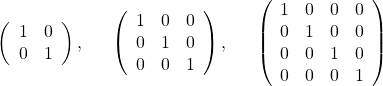
などがそうです。単位行列によく使われるアルファベットは
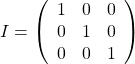
などと表します。
単位行列は、行列の世界における、数字の「1」に相当します。というのは、いかなる行列に単位行列を掛けても、行列は変化しないからです。これを実際に確かめてみましょう。
例えば
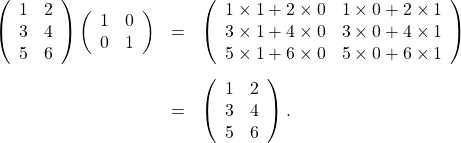
単位行列を掛ける前後で行列は変わっていませんね。同様に
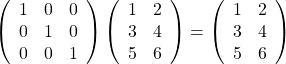
も確かめてみてください。
単位行列をベクトルにかけても同じです。

ベクトルに変化はないことが確かめられます。
行列のかけ算と単位行列が理解できると、「逆行列」を学ぶことができます。次回から何回かにわたって、「逆行列」を勉強します。
>> 行列の基本(11)逆行列1 逆行列の定義
