<< 1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17
行列のかけ算5 ABC
行列が3つ以上あるとき、それらの積について考えましょう。例えば
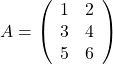
![]()
![]()
のとき、積
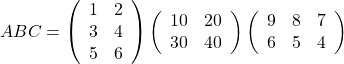
もうひとつ、計算結果のサイズがいくつになるかも、きちんと予想してください。先頭の行列
エクセルで3つの行列の積を求めるときは、ちょっとした工夫が必要です。というのも、第(6)回で用いたMMULT関数は、2つの行列の積しか求められないからです。3つ掛けたいときは、MMULT関数を入れ子にして2回使用します。
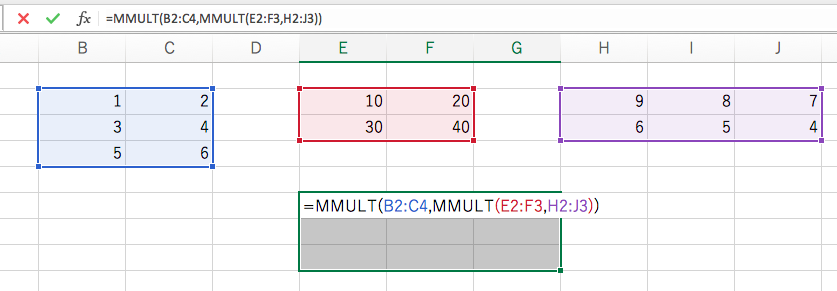
確定するときは Ctrl + Shift + Enter です。
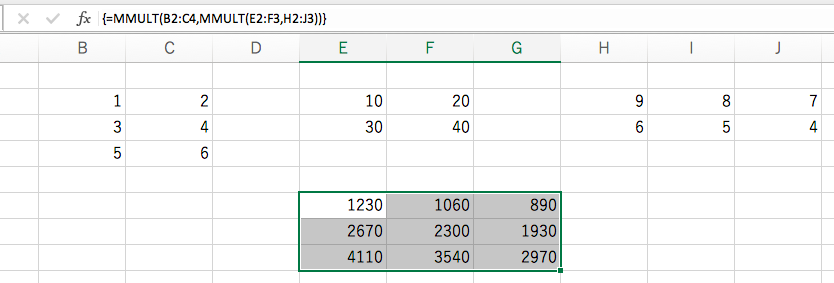
さて、5回にかけて、行列のかけ算を学んできました。行列のかけ算ができるようになったところで、次回は「行列の転置」と、それに関する大事な定理を紹介します。
>> 行列の基本(9)行列の転置
