<< 1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17
行列のかけ算2 xB
前回は、「行列と縦ベクトル」のかけ算を勉強しました。今回は、「横ベクトルと行列」のかけ算です。例えば
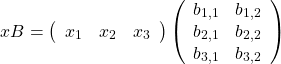
です。先行するのは横ベクトルで、行列は後方にきています。この2つの積を計算するときは、

というふうに、後方の行列を各列に区切ります。そして、ベクトルと、各列との内積を計算します。先行するベクトルのサイズと、行列の行数が一致していることが前提です。
もうひとつ例を見ておきましょう。今度は ![]() のサイズが
のサイズが ![]() です。
です。
![]()
この計算手順を図示すると、

です。先ほどとサイズは違いますが、原理は同じです。練習として、次の積を計算してみましょう。
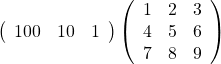
どうでしょうか。後方の行列を縦に切ることを忘れないでください。正解は
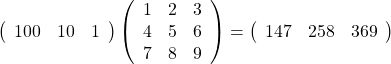
です。正しくできましたか?
次回は「行列と行列」のかけ算です。
>> 行列の基本(6)行列のかけ算3 AB
今回のポイント
横ベクトルと行列のかけ算では、行列を列に区切り、それぞれ横ベクトルとの内積を取る。
