目次

<< １，２，３，４，５，６，７，８，９，10，11，12，13，14，15，16，17

行列の「成分ごとのかけ算」


前回やったように、行列の足し算は、単に成分ごとの足し算です。しかし、「行列のかけ算」は単なる成分ごとのかけ算ではありません。そのため、仮にもし、行列を成分ごとにかけ算したいならば、はっきり「成分ごとのかけ算 (component-wise multiplication)」だと断っておく必要があります。例えば

    \begin{eqnarray*} A&=&\left( \begin{array}{cc} 1& -2 \\ 3 & 5.5 \end{array} \right)\\ \\B&=&\left( \begin{array}{cc} 10& 100 \\ 10 & 1000 \end{array} \right) \end{eqnarray*}


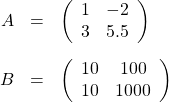
の「成分ごとのかけ算」をすると、

    \begin{eqnarray*} A\times B &=& \left( \begin{array}{cc} 1& -2 \\ 3 & 5.5 \end{array} \right) \times \left( \begin{array}{cc} 10& 100 \\ 10 & 1000 \end{array} \right)\\ \\&=& \left( \begin{array}{cc} 1 \times 10& -2\times 100 \\ 3\times 10 & 5.5\times 1000 \end{array} \right)\\ \\&=& \left( \begin{array}{cc} 10& -200 \\ 30 & 5500 \end{array} \right) \end{eqnarray*}


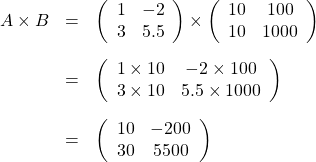
です。しかしながら、通常、「行列のかけ算」とか「行列の積」といった場合、別の物を指します。次回からその「行列のかけ算」を説明したいと思います。

>> 行列の基本（４）行列のかけ算１　Ax