ナッシュ均衡3 :お互いに最適反応
ナッシュ均衡の定義の言い方には2通りあります。1つめは「誰も逸脱するインセンティブを持たない戦略プロファイル」でした。今日はこれを少し言い換えた、2つめの定義を紹介します。言っていることは同じなのですが、場合によってはこちらの言い方が便利なのです。
「逸脱するインセンティブがない」とは、要するにベターな戦略がないということです。よって、誰も「逸脱するインセンティブがない」とは、どのプレーヤーも他のプレーヤーたちに対して最適に反応しているということと同じです。したがって、ナッシュ均衡の定義は次のように言い換えられます。
ナッシュ均衡の定義(バージョン2)
ナッシュ均衡とは、プレーヤーたちの戦略がお互いに最適反応になっている戦略プロファイルである。
この定義に基づき、第4回に登場した「宅飲みの用意をする2人」のゲームのナッシュ均衡を見つけましょう
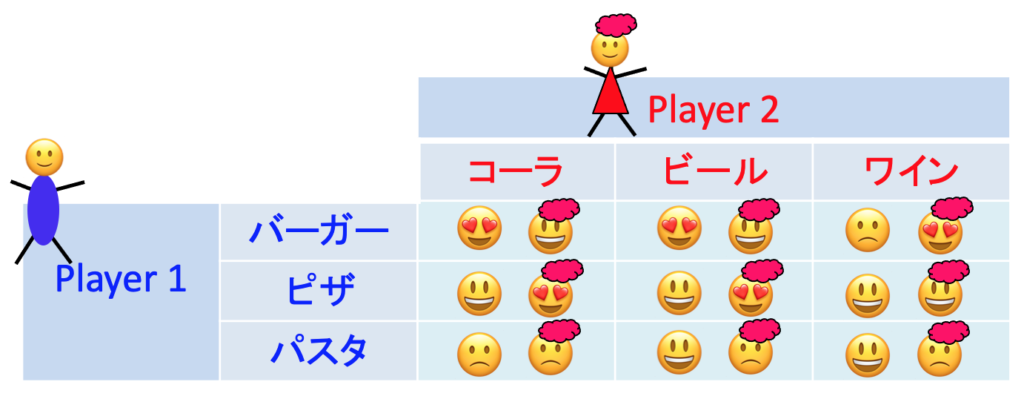
最適反応は第4回ですでに求めたので復習してください。プレーヤー1の最適反応は以下の通りです。
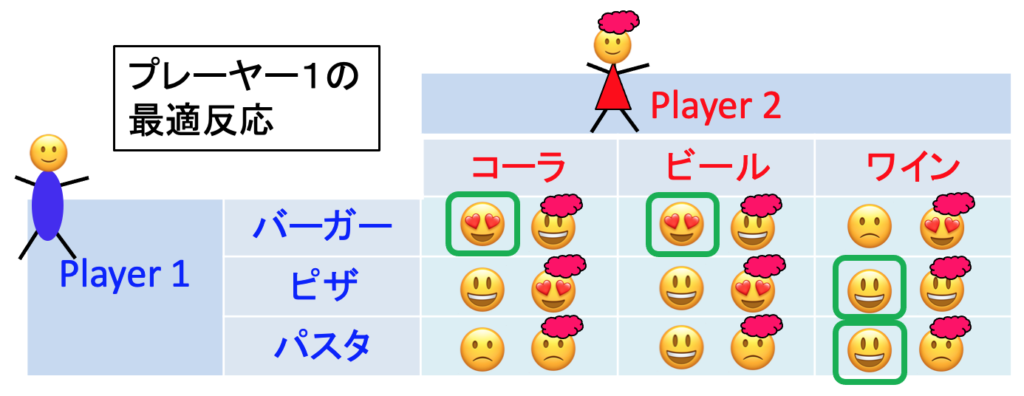
プレーヤー2の最適反応は以下の通りです。
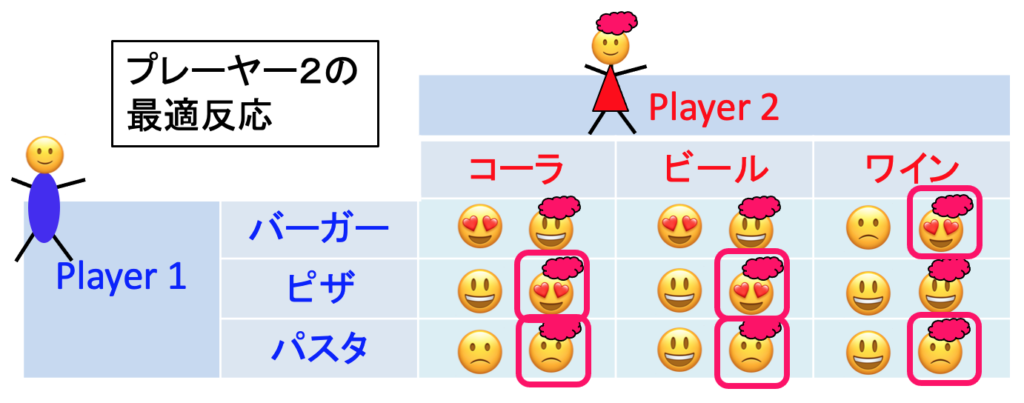
プレーヤー1と2の最適反応をともに表示すると以下のようになります。
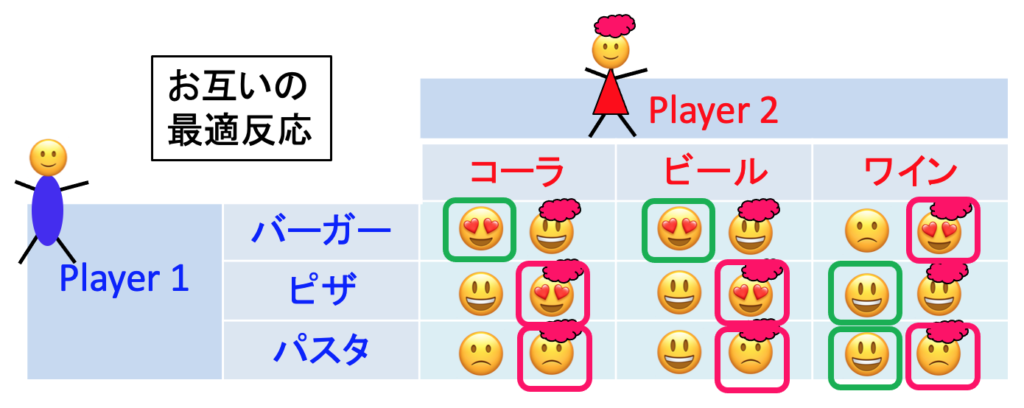
お互いに最適反応となっている戦略プロファイルは「パスタ,ワイン」です。したがって今日紹介した定義に照らせば、これがこのゲームのナッシュ均衡だと分かります。最適反応なのですから、(自分だけ)他の戦略に変えても利得が上がることはありません。したがって「逸脱するインセンティブがない」という前回の定義でもナッシュ均衡になっていることが確認できます。
このように、「相手がこれなら自分はこれで対抗」という最適反応を全て求めることができるならば、ナッシュ均衡をしらみつぶしに探すことができます。これは、後々「クールノー・ゲーム」を勉強するときに使う発想なので、ぜひ覚えておきましょう。
さて、ナッシュは1951年の論文で、「プレーヤーの人数が有限、戦略の数も有限であるゲームには、必ずナッシュ均衡が存在する」ことを数学的に証明しました。こう聞くと、「じゃんけん」や「マッチング・ペニー」にはナッシュ均衡は無いではないかと思う人がいるかもしれません。でも実際には「じゃんけん」や「マッチング・ペニー」にもナッシュ均衡がちゃんとあります。このことを説明するには、「混合戦略」の概念を用いなければなりません。それは別のシリーズで扱うことにしましょう。(終わり)
>> 混合戦略(1)
