タダ乗りゲームの混合戦略均衡５ 傍観者効果
前回は、「
人のうち１人でも行動してくれれば、みんながハッピーになれる」という状況で、倫太くんという１プレーヤーの視点に立って、混合戦略均衡を求めました。
いったん均衡を見つけたら、倫太くんの視点を離れ、一段上から眺めてみましょう。倫太くんも含めた 人のうち、誰か１人でも声を上げる確率 
はいくつでしょうか。 人それぞれ、確率 
で声を上げ、確率 
で何もしない。ということは、少なくとも誰か１人が声を上げる確率は 
です。 前回求めた 
を代入すると、「 人の学生のうち誰か１人でも声をあげる確率 」は、
となります。（
という仮定なので、 は必ず１より小さい値です。）
この を、横軸に学生数 をとって、グラフにしてみます。コスト 
が変わればグラフも変わるので、以下の図では、コストが低めの場合（
，赤線）と高めの場合（
，青線）の２種類のグラフを表示しています。今日は赤い方の折れ線を使って説明します。
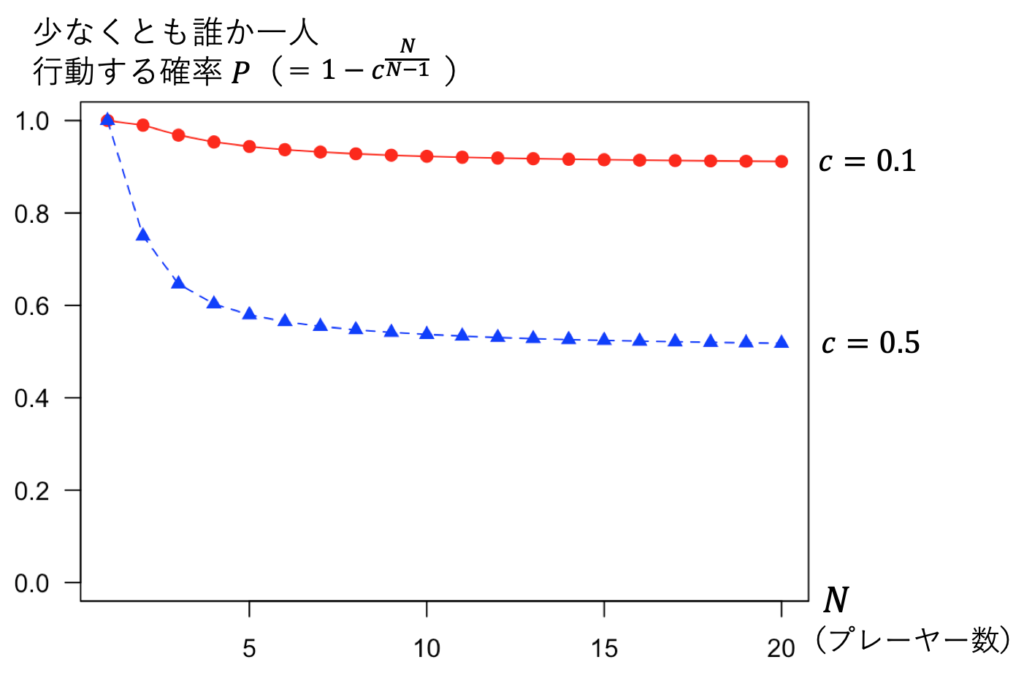
赤い折れ線は、コストが の場合です。このとき、
であれば 
です。すなわち、講義室に学生が２人しかいなければ、99%の確率でどちらかが指摘します。
そして、ここがポイントですが、 が大きくなるほど、この確率は小さくなります。０にはなりませんが、
に向かって小さくなっていくのです。100人もいる講義なら、 はおよそ90%にまで下がります。不思議なことに、プレーヤーの数が多いほど、誰か１人でも行動する確率は、低くなるのです。
いったいなぜでしょう。「大講義であるほど、声をあげるのは恥ずかしいからだ」というのは理由にはなりません。このゲームのプレーヤーたちが恥ずかしさを感じるとすればそれは で表されており、人数の多さには関係ないという仮定だからです。行動する確率が下がってしまうのは、全体の人数が多いほど、「誰かがやってくれるかも」という期待が大きくなってしまうからです。これは「傍観者効果 (Bystander effect)」と呼ばれています。
全体の人数が増加していくと、それにも増して、一人ひとりの行動する確率が減少します。傍観者効果のせいで、結局誰もやってくれないという可能性が高くなるのです。
この結果を応用すると、たくさんの人に一斉にメールをして、「誰かやってもらえませんか」とお願いするのは、賢い策ではないことが分かります。理論の想定と近い状況なら、１人か２人選んでお願いする方が、聞いてもらえる可能性が高いでしょう。
これでゲーム理論の「混合戦略均衡」に関する基本的な練習は終わりです。次回からは、「均衡」とは何かという、これまでずっと先延ばしにしてきた話に入りたいと思います。
>> 最適反応とナッシュ均衡（１）利得表１
