<< 1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17
モデルの解析解
方程式を解く際に、外生パラメータに具体的な数値を入れずに、一般的な文字のまま求めた解のことを「解析解」と言います。中学で習う「二次方程式の解の公式」が解析解の一例です。45度線モデルは連立一次方程式なので、解析解を求めることができます。
前回、式の数を最終的に2本にまで減らしました。産出![]() と消費
と消費![]() に関して
に関して

です。ここから解析解を求めるには、まず、1本目の式の消費![]() に、2本目を代入して
に、2本目を代入して![]() を消去します。
を消去します。
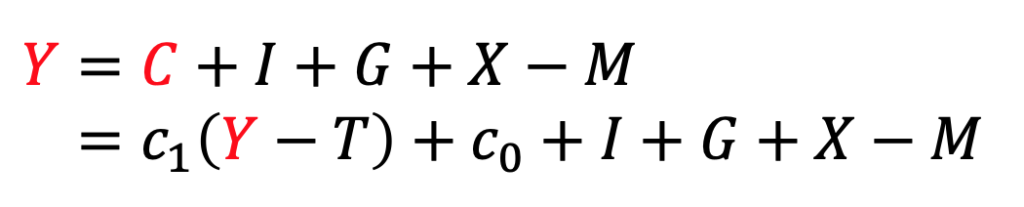
それから![]() を左辺に集めます。
を左辺に集めます。
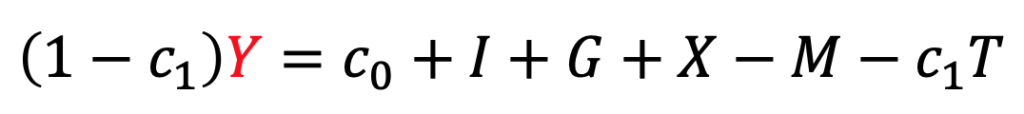
あとは両辺を![]() で割れば、産出
で割れば、産出![]() が求まります。経済学では「解だ」ということを強調するために、よくアスタリスク(*)をつけるので、ここでもそうしておきます。
が求まります。経済学では「解だ」ということを強調するために、よくアスタリスク(*)をつけるので、ここでもそうしておきます。![]() が0と1の間の数であるという仮定も思い出してください。
が0と1の間の数であるという仮定も思い出してください。
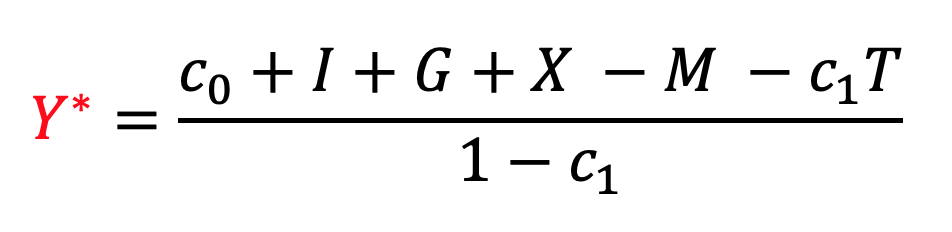
![]() を求めるには、今求めた
を求めるには、今求めた![]() を2本目の式に戻して整理するか、あるいは最初から
を2本目の式に戻して整理するか、あるいは最初から![]() を消去する代わりに
を消去する代わりに![]() を消去するのも手です。答えは
を消去するのも手です。答えは
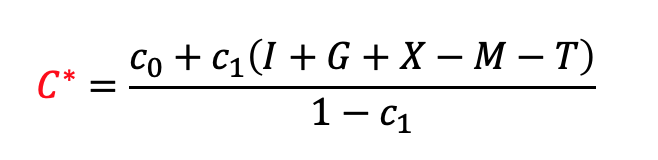
です。これで解析解![]() が求まりました。右辺には外生パラメータしかないことを確認してください。
が求まりました。右辺には外生パラメータしかないことを確認してください。
続いて、前回も出てきた比較静学をやってみましょう。政府が支出を![]() だけ増やしたら(注:経済学では、
だけ増やしたら(注:経済学では、![]() の変化分は
の変化分は![]() と記します)、均衡における
と記します)、均衡における![]() や
や![]() はどれだけ増えるでしょうか。先ほど求めた解を見ると分かります。
はどれだけ増えるでしょうか。先ほど求めた解を見ると分かります。![]() の変化は、
の変化は、![]() の変化の
の変化の![]() 倍ですし、
倍ですし、![]() の変化は、Gの変化の
の変化は、Gの変化の![]() 倍ですね。(詳細はこちら)
倍ですね。(詳細はこちら)
では政府が税金を![]() だけ増やしたらどうでしょうか。増税すると、この世界のGDPや消費は下がると思われますが、どれくらい下がるでしょうか。これも解を見れば分かります。
だけ増やしたらどうでしょうか。増税すると、この世界のGDPや消費は下がると思われますが、どれくらい下がるでしょうか。これも解を見れば分かります。![]() の変化、
の変化、![]() の変化ともに、
の変化ともに、![]() の変化の
の変化の![]() 倍となるはずです。
倍となるはずです。
これらの結果をまとめておきましょう。
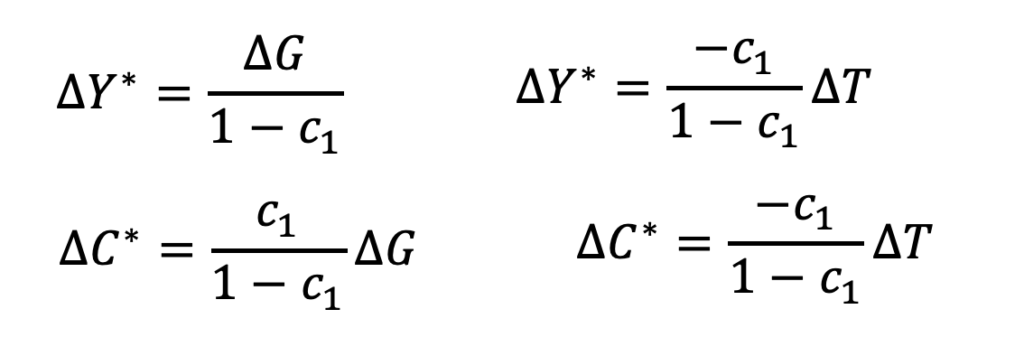
たとえば、増税![]() するとGDPは減少
するとGDPは減少![]() することが分かります。逆に、減税した場合は
することが分かります。逆に、減税した場合は![]() はマイナスなので、GDPは増加します。これが、「前ばらし」のところで予告した、45度線モデルの1つめのメッセージです。
はマイナスなので、GDPは増加します。これが、「前ばらし」のところで予告した、45度線モデルの1つめのメッセージです。
これらは結果だけ見ると「ふーん」で終わってしまいますが、実はここに、よく知られた45度線モデルの、よく知られていないメッセージが含まれています。次回はそれについてです。
>> GDPの45度線モデル(10)「乗数効果」再検証

