<< 1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17
モデル式の導出
これから「GDPの45度線分析モデル」に具体的に入っていきます。45度線モデルの世界が想定することは以下の4点です。
- 財やサービスは、消費者に消費されたり、企業の投資に使われたり、政府が使ったり、海外に輸出されたりする。
- 人々は、手取り収入が大きいほど、たくさん消費する。
- 生産は人々の所得となる。
- 需要を満たすべく生産量が決まる。
それぞれが1本の式で表されるので、45度線モデルは式4つの連立方程式となります。これから式を1つずつ導出しますが、文字がたくさん出てくるので、どの文字が何を表すのか、できるだけ頭に入れながら進んでください。
1つめの式
まずは一国で作られた財・サービスが使用される側、つまり「需要・支出」の内訳を表す式です。第2回で説明したとおり、需要![]() の内訳は、「民間消費
の内訳は、「民間消費![]() 」,「投資
」,「投資![]() 」,「政府支出
」,「政府支出![]() 」,そして「海外」の4つです。海外からの需要とは、要は海外に輸出される農産物や工業製品のことなのですが、より正確には、輸入される量を引いた「純輸出」で測ります。輸出を
」,そして「海外」の4つです。海外からの需要とは、要は海外に輸出される農産物や工業製品のことなのですが、より正確には、輸入される量を引いた「純輸出」で測ります。輸出を![]() 、輸入を
、輸入を![]() で表すなら、
で表すなら、![]() です。こうして、日本で生み出された財やサービスに対する需要
です。こうして、日本で生み出された財やサービスに対する需要![]() の内訳式は
の内訳式は
(1) ![]()
となります。
2つめの式
45度線モデルでは、消費者は「手取り収入が高いほど、たくさん消費をする」と想定されます。具体的には、所得を
(2) ![]()
で決まると仮定されます。
切片
3つめの式
3つめは、この国の人々の所得が産出
(3) ![]()
です。「新たに生み出された価値が、誰かしらの所得になる」という考え方は第3回でも紹介しました。
4つめの式
最後は、産出
(4) ![]()
です。需給を満たすように生産が決まるという仮定です。3つめの式と合わせると「所得=産出=需要」なので、GDPの三面等価が、45度線モデルの世界でも成立していることが分かります。
まとめると、45度線モデルは、4本の式の連立方程式となります。
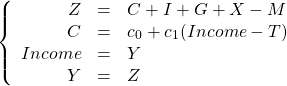
このモデルの内生変数は
4本の式の意味は分かりましたか。次回は実際にこのモデルを解いてみましょう。
>> GDPの45度線モデル(8)モデルの数値例

