<< １，２，３，４，５，６，７，８，９，10，11，12，13，14，15，16，17
モデルの数値例
経済学のモデルは、一つ一つの式が経済的な解釈を持った連立方程式です。式の数と内生変数の数が必ず一致しており、解が１つ出てきます。連立方程式の解を経済学では「均衡」と呼びます。
GDPの45度線モデルも同じです。前回の内容をまとめると、45度線モデルは以下のような連立方程式となります。
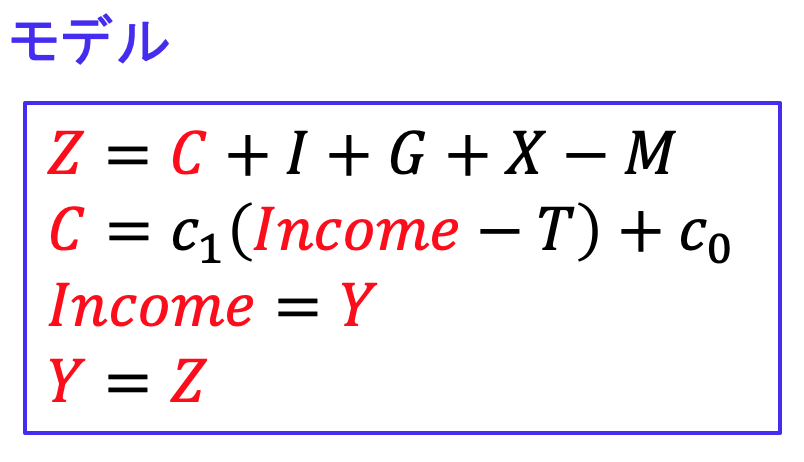
赤い文字が４つの内生変数です。意味は、Zが需要、Cが消費、Incomeが所得、Yが産出でした。残りの変数は外生変数で、Iが投資、Gが政府支出、Xが輸出、Mが輸入、Tは税金、
が消費関数の傾き（限界消費性向）で、
が切片でした。式の説明はここでは繰り返しません。
この連立方程式を解いてみましょう。まず、３、４番目の式を使って、IncomeとZは消去してしまいます。そうすると、式が２本だけになった連立方程式となります。
外生変数の値をためしに
，
，
，
，
，
だとします。税金はなし、企業の投資は50兆円、政府支出は30兆円、純輸出は20兆円といった具合です。
このとき、
に関する連立一次方程式を解くと、
, 
が出てきます。GDPは500兆円、うち消費が400兆円です。
「比較静学 (comparative statics)」とは、環境や政策が変化したときに経済の均衡がどう変わるか、つまり外生変数の値が変化したときに方程式の解がどう変わるかを調べるエクササイズのことを言います。例えば、上の数値例で、政府が景気対策のために税金は変えずに政府支出だけ20兆円増やしたら、解はどう変わるでしょうか。から
となるので、これを代入して方程式を解き直すと、
, 
が出てきます。Gを上げる前の解と比べると、GDPは50兆円増えています。政府支出は20兆円しか増やしていないのに、GDPは50兆円増えたということで、このモデル世界でも乗数効果が生じることが確認できます。
ここでは外生変数に具体的な数字を代入して計算してみました。次回は具体的な数字を入れずに解いてみましょう。
>> GDPの45度線モデル（９）モデルの解析解
