確率変数が n 個の場合
前回は確率変数が３個ある場合の分散公式を勉強しました。今回は n 個ある場合です。n 個の確率変数 
の線型結合は、係数を 
とおけば、 
と表されます。分散はいくつになるでしょうか。
見た目は難しくなりますが、３個の場合と基本的に同じです。確率変数が n 個あるので、まずは分散の項が n 個出てきます。さらに、確率変数のペアの数だけ共分散の項が出てきます。
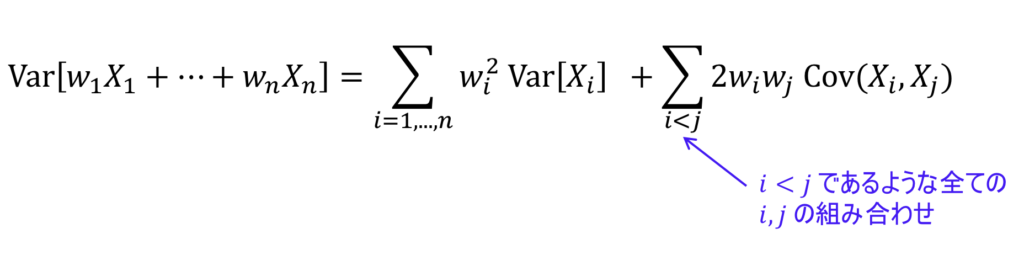
ここで「
であるような 
と 
の組み合わせ」とは、たとえば１と２、１と３、２と３・・・のような組み合わせを漏らすことなく全て、という意味です。もし、和のシグマ記号のこのような使い方に慣れていなければ、こちらを参考にしてください。シグマ記号の意味が分かれば、この公式は確率変数が３つの場合の延長に過ぎないことが分かります。
ただこの公式は、見た目がゴチャゴチャしていますね。エクセルで計算するにも、式を入力するだけで時間がかかりそうです。もう少しスッキリあらわすことはできないでしょうか。それが次回のテーマです。
次回は、n 個の確率変数の線型結合の分散の公式を、和の記号シグマを使わずに、スッキリ表す方法を勉強します。
>> 和の分散公式（６）行列で表した分散公式