目次へ

<< １，２，３，４，５，６

aX+bY の分散の公式


次に、確率変数X, Y の前に係数がついている場合の分散公式です。2X+3Y のように、確率変数に係数をつけて足し合わせたものを、確率変数の「線形結合」と呼びます。線型結合は、期待値に関しては

    \begin{eqnarray*} E[2X + 3Y] = 2E[X] + 3E[Y] \end{eqnarray*}


のような分解が可能です（線型結合の期待値を参照）。しかし、分散や標準偏差ではそのような分解はできません。


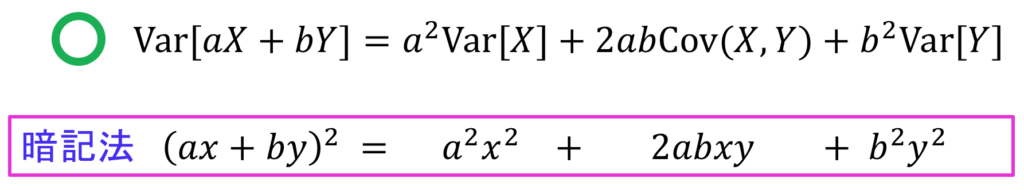
線型結合の分散の公式を以下に示します。この公式は、中学の数学で教わる (2x+3y)^2 のような式の展開を思い出すと、覚えやすいでしょう。係数を a, b で表せば




X と Y の標準偏差から、aX+bYの標準偏差が求まると思いがちですが、それは間違いです。X と Y を合わせたリスクを求めるには、両者の相関関係をふまえ、分散公式を経由しないといけないのです。（*注1）


１つ練習問題をやってみましょう。


問題
X と Y の標準偏差が \sigma_X=2.50, \sigma_Y=1.56, 両者の相関係数が \rho_{X,Y}=0.984 であると分かっている。このとき、0.5X + 0.5Y の標準偏差はいくつか。


解答のポイントは、まず分散と共分散を求め、それから公式を使うという点です。このことを図にしておきます。



（解答はこちら）


次回は確率変数が３つある場合の分散公式です。

>> 和の分散公式（４）確率変数が３つの場合

*注1：
ちなみに定数項は分散には影響しません。すなわちa, b を定数とすれば

    \begin{eqnarray*}\mbox{Var}[X+b] = \mbox{Var}[X] \end{eqnarray*}



    \begin{eqnarray*}\mbox{Var}[aX+b] &=& \mbox{Var}[aX] \\&=& a^2 \mbox{Var}[X]\end{eqnarray*}


が成立します（証明は省略）。これは、分散が「ばらつき」の指標であることを覚えていれば直観的なことです。日本中のすべての人に5cmの靴を履かせれば、身長の平均は5cm上がるでしょう。一方、みんな5cm上がるなら、ばらつきは変わりません。


問題の解答（戻る）

（「確率変数の平・分・共・標・相」の数値例を使っているため、少数の四捨五入による若干の誤差があります。）

公式を使うために、まずは X と Y の分散と、両者の共分散を求めます。分散は標準偏差の２乗なので、

    \begin{eqnarray*} \mbox{Var}(X)&=&\sigma^2_X = (2.50)^2 = 6.24\\\mbox{Var}(Y)&=&\sigma^2_Y = (1.56)^2 = 2.44 \end{eqnarray*}


また、相関係数の定義から共分散を逆算すると

    \begin{eqnarray*} \mbox{Cov}(X, Y) &=& \rho_{X, Y}\sigma_X\sigma_Y\\&=& 0.984 \times 2.50 \times 1.56\\ &=& 3.84 \end{eqnarray*}


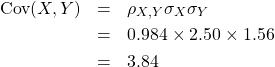
（共分散を２つの標準偏差で割ったものが相関係数だからです。）

分散と共分散が分かったら、上の分散公式 (a=b=0.5) に当てはめて、

    \begin{eqnarray*} \mbox{Var}(0.5X + 0.5Y)&=&(0.5)^2 \mbox{Var}(X) + 2(0.5)(0.5)\mbox{Cov}(X,Y) + (0.5)^2 \mbox{Var}(Y) \\ &=& 4.09 \end{eqnarray*}


が出てきます。よって標準偏差は

    \begin{eqnarray*} \mbox{Std}(0.5X+0.5Y)=\sqrt{4.09} = 2.02 \end{eqnarray*}


です。