<< 1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17
モデルを改良する練習
物理学に出てくるモデルと違い、経済学に出てくるモデルは、真理ではありません。あくまで、複雑な現実の一面だけに焦点を当てた、シミュレーション世界です。したがって、単純化されていることが経済学モデルの良さなのですが、使用目的にかんがみて不満足な点があると思われる場合は、モデルを少し複雑化します。連立方程式の一部を変更したり、新たに内生変数を付け加えて式の数を増やしたりするのです。
今回は、45度線モデルで、そのような「モデルの改良」をやってみましょう。その前に基本モデルの復習をしておくと、式は
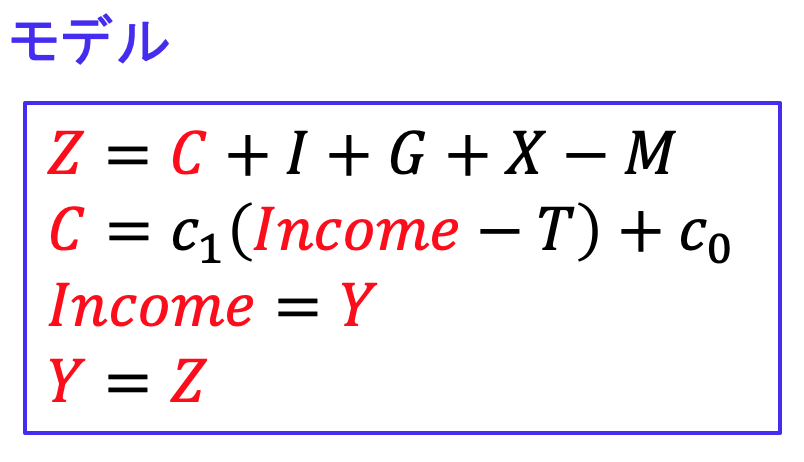
でした。赤い文字が内生変数で、意味はYが産出、Incomeが所得、Zが需要、Cが消費でした。あとは外生変数で、Iが投資、Gが政府支出、Xが輸出、Mが輸入、Tが税金、![]() が消費関数の傾きで、
が消費関数の傾きで、![]() が切片でした。これらを出発点にいくつかの改良を試みますが、話を簡単にするため、ここからは輸出入の差はゼロ(
が切片でした。これらを出発点にいくつかの改良を試みますが、話を簡単にするため、ここからは輸出入の差はゼロ(![]() )とみなします。
)とみなします。
4つの例をやってみますが、いずれも連立方程式を改良するところまでしかやりません。経済学では「式を立てること(“モデル化”)」と「式を解くこと」は異なる能力とみなされます。式を解く方は、今日はやりません。
例1.投資の内生化
統計上、民間の投資(企業の投資+家計の住宅投資)は一国のGDPの2割を占めます。したがって、投資![]() が外生というのは、やはりモデルとして物足りません。そこで
が外生というのは、やはりモデルとして物足りません。そこで![]() を内生変数にしましょう。ただ、企業の投資がどう決まるかを式化するのは難しいので、ここでは家計の住宅投資だけを式化します。具体的には投資
を内生変数にしましょう。ただ、企業の投資がどう決まるかを式化するのは難しいので、ここでは家計の住宅投資だけを式化します。具体的には投資![]() が
が
![]()
と決まるとします。ここで、![]() は切片で、
は切片で、![]() は傾きです。
は傾きです。![]() の部分が家計の所得に依存する住宅投資、
の部分が家計の所得に依存する住宅投資、![]() の部分が家計の所得に依存しない企業の設備投資です。この式が加わった結果、45度線モデルの連立方程式は
の部分が家計の所得に依存しない企業の設備投資です。この式が加わった結果、45度線モデルの連立方程式は
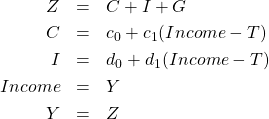
となります。これで![]() が内生変数に加わりました。内生変数は
が内生変数に加わりました。内生変数は![]() です。式の数と内生変数の数が、ともに5個で一致していることを確認してください。
です。式の数と内生変数の数が、ともに5個で一致していることを確認してください。
例2.比例税
さて、基本の45度線モデルでは税金![]() は比例税ではありませんが、ここでは税金を税率
は比例税ではありませんが、ここでは税金を税率 ![]() の所得税であると仮定してみましょう。つまり
の所得税であると仮定してみましょう。つまり
![]()
です。たとえば![]() であれば、所得の2割を税金として徴収される社会です。このとき、税引き後所得は
であれば、所得の2割を税金として徴収される社会です。このとき、税引き後所得は![]() となります。よって45度線モデルの連立方程式は、
となります。よって45度線モデルの連立方程式は、![]() を消去してしまえば
を消去してしまえば
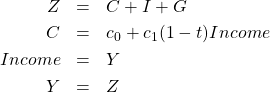
となります。内生変数は![]() の4個です。(もし最初の
の4個です。(もし最初の ![]() も入れて式を5本とするなら、
も入れて式を5本とするなら、![]() も内生変数に入ります。)これで、政府が税率
も内生変数に入ります。)これで、政府が税率 ![]() を下げた場合、どれくらい税収が下がるかを分析できます。所得税率を下げてもGDPが増えるなら、そこまで税収は減らないかもしれません。実際のところはどうなのか、シミュレーションできるモデルです。
を下げた場合、どれくらい税収が下がるかを分析できます。所得税率を下げてもGDPが増えるなら、そこまで税収は減らないかもしれません。実際のところはどうなのか、シミュレーションできるモデルです。
例3.比例税で均衡財政
さて、先の比例税のモデルでは税率 ![]() は外生変数でしたが、今度は
は外生変数でしたが、今度は ![]() を内生変数に変えてみましょう。政府支出
を内生変数に変えてみましょう。政府支出 ![]() は福祉や教育サービスなどのために確定していて変えようがなく、しかも法律で「政府は借金してはいけない」と定められている状況を考えてください。そうすると、政府は
は福祉や教育サービスなどのために確定していて変えようがなく、しかも法律で「政府は借金してはいけない」と定められている状況を考えてください。そうすると、政府は ![]() と同じだけの税収を集める必要があります。もはや税率
と同じだけの税収を集める必要があります。もはや税率 ![]() は任意に決められるパラメータではありません。所得税の税収が
は任意に決められるパラメータではありません。所得税の税収が ![]() に等しくなるように、税率を決めなければならないのです。この場合45度線モデルの連立方程式は
に等しくなるように、税率を決めなければならないのです。この場合45度線モデルの連立方程式は
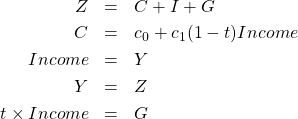
となります。5つめの式が、均衡財政を要求する式です。内生変数は ![]() の5つです。
の5つです。
例4.消費税
最後に、税金が税率 ![]() の消費税の場合を考えてみましょう。つまり
の消費税の場合を考えてみましょう。つまり ![]() ということです。45度線モデルの連立方程式は
ということです。45度線モデルの連立方程式は
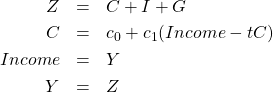
となります。内生変数は ![]() の4つです。
の4つです。
どうでしたか。このように、ちょっとした改良で済む場合は、モデルを改良したうえで式を解き直したり、比較静学を行ったりします。
一方、モデルへの批判が、モデルをちょっと改良するだけでは対処できない場合は、全く新しいモデルを作らなければなりません。そこで私たちも、そろそろ45度線モデルを卒業し、もっといろいろなモデルを学んでいくことにしましょう。

