<< 1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17
貯蓄のパラドックス
今回のポイント
民間貯蓄の定義は ![]() であり、それは
であり、それは ![]() に等しい。
に等しい。
貯蓄率を上げても、貯蓄は増えない。
「民間貯蓄」とは、人々が税引き後所得![]() のうち、消費せずに取っておく分のことです。45度線モデルでは
のうち、消費せずに取っておく分のことです。45度線モデルでは![]() がこれに相当しますが、計算するといくつになるでしょうか。
がこれに相当しますが、計算するといくつになるでしょうか。
内生変数である![]() と
と![]() は45度線モデルの連立方程式を解けば求まるので、それを
は45度線モデルの連立方程式を解けば求まるので、それを![]() に代入すれば、民間貯蓄も求まります。でも、実はもっと簡単に求める方法があります。それをこれから説明しましょう。
に代入すれば、民間貯蓄も求まります。でも、実はもっと簡単に求める方法があります。それをこれから説明しましょう。
第7回の45度線モデルの連立方程式を思い出してください。まず所得![]() は需要
は需要![]() に等しく、その
に等しく、その![]() の内訳は
の内訳は![]() ということでしたから、これを民間貯蓄の式の
ということでしたから、これを民間貯蓄の式の![]() に代入します。すると
に代入します。すると![]() がうまい具合に消えて、結局
がうまい具合に消えて、結局![]() だけが残ります(導出はこちら)。民間貯蓄を求める過程では、
だけが残ります(導出はこちら)。民間貯蓄を求める過程では、![]() と
と![]() は求めるまでもなく、どのみち消えてしまうのです。出てきた結果をまとめると、民間貯蓄は
は求めるまでもなく、どのみち消えてしまうのです。出てきた結果をまとめると、民間貯蓄は
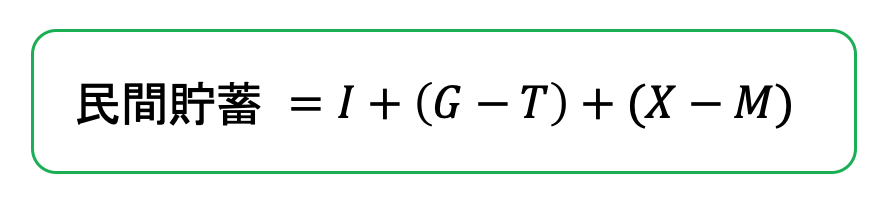
となります。![]() は企業の投資、
は企業の投資、![]() は政府の「財政赤字」で、
は政府の「財政赤字」で、![]() は「貿易黒字」です。民間貯蓄がこの3つの合計に等しいというのは、理屈のうえでも合っています。というのは、企業の投資には資金が必要ですし、政府が財政赤字を出すには国民から借金をする必要があります。また、輸出が輸入を上回れば、差額は海外に投資されます。民間貯蓄は、家計が企業に投資する分、政府に投資する分、海外に投資する分の3つに分かれるのです。
は「貿易黒字」です。民間貯蓄がこの3つの合計に等しいというのは、理屈のうえでも合っています。というのは、企業の投資には資金が必要ですし、政府が財政赤字を出すには国民から借金をする必要があります。また、輸出が輸入を上回れば、差額は海外に投資されます。民間貯蓄は、家計が企業に投資する分、政府に投資する分、海外に投資する分の3つに分かれるのです。
面白いのは、民間貯蓄の式に、限界消費性向![]() が出てこないという事実です。
が出てこないという事実です。![]() は可処分所得が増えたとき、人々がそのうちのどれだけを消費にまわし、どれだけを貯蓄にまわすかを決めるパラメータです。
は可処分所得が増えたとき、人々がそのうちのどれだけを消費にまわし、どれだけを貯蓄にまわすかを決めるパラメータです。![]() が高ければ消費にまわす割合が大きいので、貯蓄は小さくなりそうです。それなのに、貯蓄はあくまで
が高ければ消費にまわす割合が大きいので、貯蓄は小さくなりそうです。それなのに、貯蓄はあくまで![]() で、
で、![]() の大きさと無関係であるというのは一見不思議ですね。これは実は、「貯蓄のパラドックス」と呼ばれる現象が、45度線モデルの世界でも起こることを表しています。
の大きさと無関係であるというのは一見不思議ですね。これは実は、「貯蓄のパラドックス」と呼ばれる現象が、45度線モデルの世界でも起こることを表しています。
貯蓄のパラドックスとは、「みんなが貯蓄しようとすると、貯蓄は増えない」という、何とも逆説的な可能性を指す言葉です。根拠は単純で、ある人が倹約すると、その他の人の収入が減ってしまうからです。逆に、誰かがアート作品や映画、美容院や外食などに消費すれば、それは別の誰かの所得になります。45度線モデルの世界では、![]() が高い社会は、消費も所得も大きい社会です。そうして、所得と消費の差は、
が高い社会は、消費も所得も大きい社会です。そうして、所得と消費の差は、![]() が大きい社会も小さい社会も同じになるため、結果的に貯蓄に影響を与えないのです。
が大きい社会も小さい社会も同じになるため、結果的に貯蓄に影響を与えないのです。
一般に「ああすればこうなるはず」という理論的可能性を、モデルというシミュレーション世界で再現しようとしたとき、いつもうまくいくわけではありません。「風を強くすれば旅人のマントは吹き飛ぶ」と思ってシミュレーションしてみたら、当てが外れるということもしばしばです。貯蓄のパラドックスは理論的可能性に過ぎませんが、少なくとも45度線モデルの世界では再現することができました。
さて、45度線モデルの主張は、当然、モデルが想定する数々の仮定に依存しています。次回からは、45度線モデルの仮定に対する批判の例を見ながら、モデルに基づいて議論するという「経済学の作法」を体験してみましょう。
>> GDPの45度線モデル(12)モデルの仮定を批判する1:近視眼的な消費者

