債券価格の変化
「債券価格と金利の関係」シリーズでは、割引債の価格とその債券の金利は、基本的には「因果関係」ではなく「表裏一体の関係(同値関係)」であることを強調しました。たとえば、額面10,000円、満期10年、現在の価格が ![]() の割引債の金利は、次の式を満たす
の割引債の金利は、次の式を満たす ![]() です。
です。
![]()
ここで、金利
この「割引債の価格と金利」の表裏一体の関係は、「クーポン債の価格と最終利回り」についても言えます。たとえば、額面10,000円、満期3年、クーポンレート4%、現在の価格が
![]()
価格が下がることを、「利回りが上がった」と言ったりします。価格が下がることと利回りが上がることは、1つのことを言い換えたに過ぎません。
債券価格を金利の関数と見る
さて、ここで発想を転換させて、無理やり「![]() は
は ![]() の関数」と見てみましょう。
の関数」と見てみましょう。![]() は世の中の金利水準を表していると思ってください。「金利の期間構造」は満期に依らず一定とします。 ストーリーはこうです。まず、世の中の金利水準が金融市場の動向で先に決まります。あなたの保有している債券の価格が、その影響を受けて変動します。日本の賃金水準が上がったせいで、あなたのバイト先の賃金も幾らか上がるようなイメージです。
は世の中の金利水準を表していると思ってください。「金利の期間構造」は満期に依らず一定とします。 ストーリーはこうです。まず、世の中の金利水準が金融市場の動向で先に決まります。あなたの保有している債券の価格が、その影響を受けて変動します。日本の賃金水準が上がったせいで、あなたのバイト先の賃金も幾らか上がるようなイメージです。
世の中の金利が変化したとき、あなたの保有している債券はどれくらい価格変動の影響を受けるのか。ためしに今、金利の期間構造は ![]() で一定、つまり、1年物、2年物、3年物・・・の金利が全て
で一定、つまり、1年物、2年物、3年物・・・の金利が全て ![]() であるいう前提で、上記の「額面10,000円、満期3年、クーポンレート4%の債券」の現在価格をグラフにしてみましょう。つまり
であるいう前提で、上記の「額面10,000円、満期3年、クーポンレート4%の債券」の現在価格をグラフにしてみましょう。つまり
![]()
という関数を、
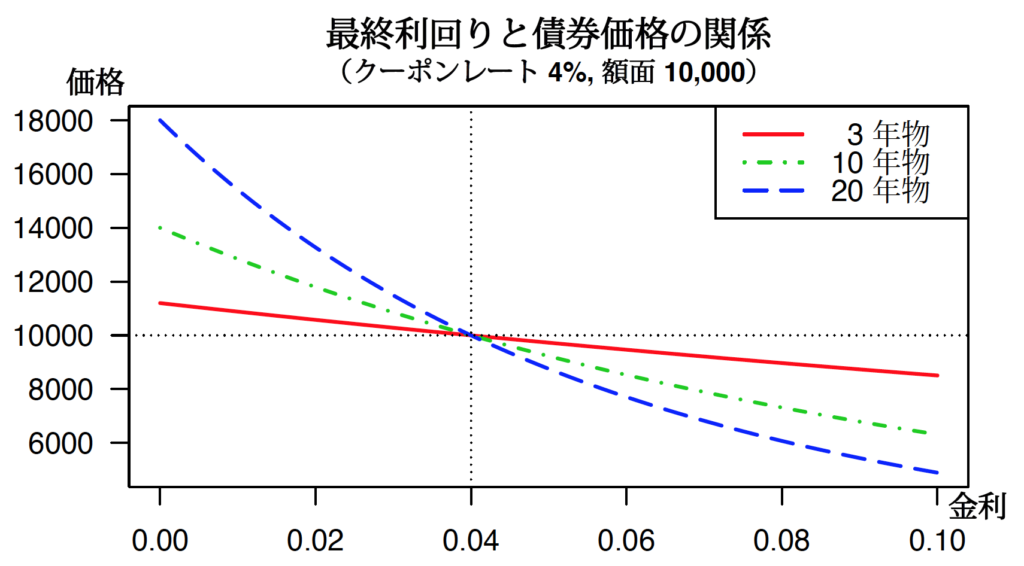
金利 ![]() が上がるほど債券価格が下がる様子が分かります。あなたが「満期3年、クーポンレート4%」の債券を保有していた場合、世の中の金利が上下したときに、価格がどれだけ上がったり下がったりするかが、このグラフから予想できます。
が上がるほど債券価格が下がる様子が分かります。あなたが「満期3年、クーポンレート4%」の債券を保有していた場合、世の中の金利が上下したときに、価格がどれだけ上がったり下がったりするかが、このグラフから予想できます。
価格変化と「年限」
世の中の金利が上がると、あなたの保有している債券の価格も下落するのですが、その下落幅は、債券の年限に依存します。同じ額面とクーポンレートで、満期だけが異なる債券どうしを比較した場合、金利が変化したときの価格の変化は、年限が長い債券ほど大きくなります。理由は、遠い将来のキャッシュフローであるほど、金利を何乗もして割り引くからです。
上の図では、満期までの年数が10年の債券を緑色の線、20年の債券を青色の線で表しています。金利が下がれば価格が上がり、金利が上がれば価格が下がるという点では満期3年の債券と同じですが、価格の変わり方はずっと大きいことに気がつきます。
金利 ![]() が変化したとき、クーポン債の価格
が変化したとき、クーポン債の価格 ![]() はどれくらい変化するのか。これの答えのキーワードとなるのが「デュレーション (duration)」です。これに関してはまたの機会に説明します。
はどれくらい変化するのか。これの答えのキーワードとなるのが「デュレーション (duration)」です。これに関してはまたの機会に説明します。
