X+Yの分散の公式
今回は確率変数の「和の分散公式」を紹介します。予備知識として、分散、共分散、標準偏差、相関係数を、「確率変数の平・分・共・標・相」のシリーズでしっかり身につけてください。
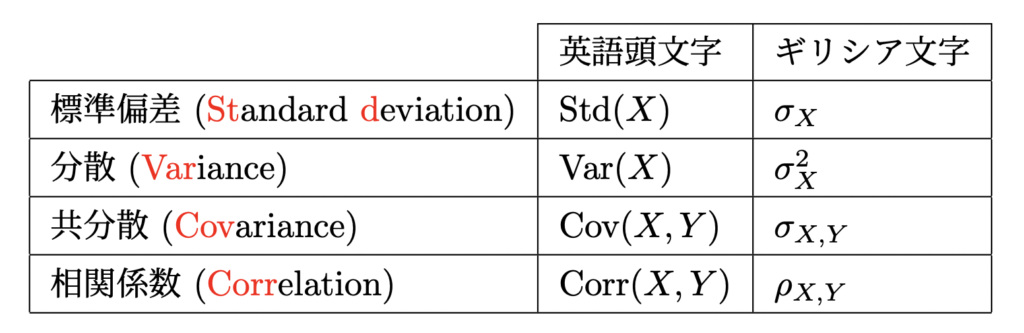
まずは、慣例として使われる表記のまとめです。今、
や 
は確率変数とします。標準偏差以下、それぞれ英語の頭文字を使う表し方と、ギリシア文字を使う表し方の２通りがあるので、その両方に慣れてください。
はシグマ、
はロウと読みます。
通常は 
などと手短かに表しますが、「
の標準偏差」などの長い表現の場合、
と書くのはやや不格好なので、Std()を用います。
正しい公式の前に、分散や標準偏差に関する典型的な間違いを、以下にバッテン付きで書いておきます。
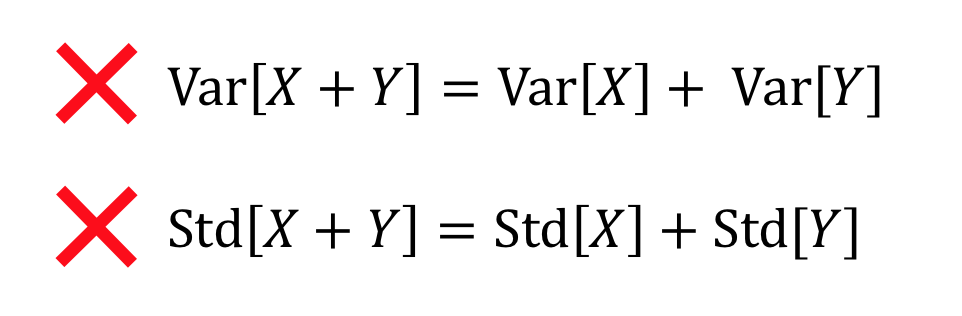
これらの式は誤りです。前回説明したように、リスクは単純に足せません。, 個々のリスクと、和 
のリスクをつなぐ正しい公式が、以下に示す「和の分散公式」です。
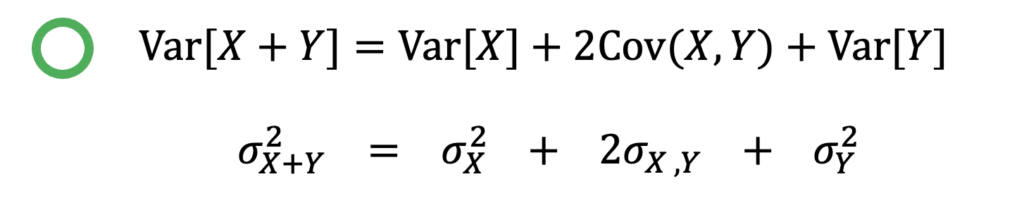
２つの式は、表記が異なるだけで、意味は同じです。一見複雑に見える公式ですが、中学で習う「和の２乗の展開公式」に見た目がとても似ているので、それが暗記法として使えます。
中学１年生が当初、和の２乗の展開で 
の項を忘れがちなように、大学生も初めは分散公式の 2Cov
の項を忘れがちなので気を付けましょう。
「確率変数の平・分・共・標・相」のシリーズの数値例を使って練習してみましょう。
Var()=6.24，Var()=2.44，Cov(
)=3.84 のとき、上の公式を使って Var() を計算してください。（正解は16.36です。）
この公式に共分散 Cov が出てくることの意味を、直観的に理解しましょう。ここがまさに、前回話した「ビール屋＆アイスクリーム屋」の組み合わせと「輸入業＆輸出業」の組み合わせの違いに関わるところです。ビール屋とアイスクリーム屋だと、売上げに高い正の相関があるので、共分散は正の値になります。だから合計売上げの分散は、個々の分散の和よりも大きくなります。一方、輸入業と輸出業のように、売上げに負の相関がある場合は、共分散は負の値になります。だから合計の売上げの分散は、個々の分散の和よりも小さくなるのです。共分散の項が、和の分散公式の一番のミソです。
和の分散公式は、複数のビジネスや投資を組み合わせてリスクを管理しようという文脈で使われます。そこで次回は、公式を一歩発展させ、 や に係数がついたバージョンを勉強します。
>> 和の分散公式（３）aX+bYの分散の公式