コンソル債の割引現在価値
普通の債券では、やがて満期がおとずれます。ところが満期が永久におとずれない債券も存在します。「コンソル債」と呼ばれる債券です。コンソル債とは、例えば未来永劫、毎年10万円支払われる、というような債券です。18世紀にイギリス政府が発行したコンソル債が有名です。
これからずっと、毎年10万円が支払われる国債が発行されたとしたら、それはいくらでしょうか。これも割引率によって決まります。仮に割引率（金利）が 
で一定であるとしましょう。すると１年後の10万円の現在価値は
万円，2年後の10万円の現在価値は
万円・・・というふうになり、コンソル債の現在価値は
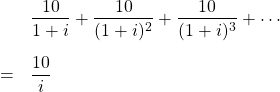
イコールの所には、等比数列の無限和の公式を用いています。
もし金利が１％の世界（
）であったとすると、このコンソル債の価値は 
万円ということになります。つまり、日本政府が毎年10万円支払うというコンソル債が発行されたとき、これを購入するなら価格は1,000万円です。また、過去に発行したコンソル債を、政府が投資家から買い戻したいと考えたなら、1,000万円払わなければならないでしょう。永久的に毎年支払われるお金を足し合わせる「割引現在価値」の考え方は、コンソル債の価格以外にも応用できます。例えばあなたが経営する貸し倉庫に、重さ１トンの漬物石を保管してほしいという客がやってきました。保管料は年間10万円で、本来なら毎年末に請求します。ところが、その客は「これから永久に保管してもらうための料金を一括で支払いたい」と言ったとします。この場合、あなたはいくら要求すべきでしょうか。ここでも「割引現在価値」の考え方が応用できます。
類似の例を挙げましょう。ある人がお寺に自分自身のお墓を購入したいと思ったとします。この人が亡くなったあとも、未来永劫残るお墓です。お墓の維持費には、年間10万円かかるとします。このお寺はお墓の値段としていくら受け取るべきでしょうか。
どちらも、「これから毎年ずっと10万円」の現在価値を求める問題です。ストーリーは異なっても、コンソル債の場合と同じ計算式を用いることができます。（金利が
ならば1000万円ということになります。）次回はこの「無期限の場合」で、割賦価値を考えます。
>> 現在価値と割賦価値（５）無期限の割賦